Niech [math]a,b[/math] będą dowolnymi elementami (zbiorami). Przez parę uporządkowaną [math]\left( a,b\right)[/math] rozumiemy zbiór [math]\left\{ \left\{ a\right\},\left\{ a,b\right\} \right\}.[/math]
Uwaga: [math]\left( a,a\right) =\left\{ \left\{ a\right\},\left\{ a,a\right\} \right\}=\left\{ \left\{ a\right\},\left\{ a \right\}\right\}=\left\{ \left\{ a\right\} \right\}.[/math]
Parę uporządkowaną można też zdefiniować w inny sposób. Chodzi jednak o to, by dla takich par spełniona była własność zapowiedziana w pierwszym rozdziale, która mówi, że jeśli jedna para uporządkowana różni się od drugiej pary, choć na pierwszej czy choć na drugiej współrzędnej, to te pary uporządkowane są różne. A więc pokażemy, że przy naszej definicji pary uporządkowanej, zachodzi:
Twierdzenie 1. Dla dowolnych [math]a,b,c,d[/math], mamy:
[math]\left( a,b\right)=\left( c,d\right) \Longleftrightarrow \left\{ \left\{ a\right\},\left\{ a,b\right\} \right\}=\left\{ \left\{ c\right\},\left\{ c,d\right\} \right\}\Longleftrightarrow a=c \wedge b=d.[/math]
Oczywiście pierwsza równoważność to tylko zastosowanie definicji, interesuje nas druga równoważność, a w zasadzie implikacja [math]\Longrightarrow[/math].
Dowód: Załóżmy zatem, że [math]\left\{ \left\{ a\right\},\left\{ a,b\right\} \right\}=\left\{ \left\{ c\right\},\left\{ c,d\right\} \right\}.[/math]
Mamy [math]\left\{ a\right\} \in \left\{ \left\{ a\right\},\left\{ a,b\right\} \right\}[/math], więc [math]\left\{ a\right\} \in \left\{ \left\{ c\right\},\left\{ c,d\right\} \right\}[/math], a więc [math]\left\{ a\right\}=\left\{ c\right\}[/math] lub [math]\left\{ a\right\}=\left\{ c,d\right\}[/math]. W pierwszym przypadku [math]a=c[/math], ale w drugim również jest tak, mamy bowiem, z zasady równości zbiorów , że [math]c \in \left\{a\right\}[/math], a więc [math]c=a[/math]. Wiemy już, ze pierwsze współrzędne równych par są równe:
[math]\left( a,b\right)=\left( a,d\right)[/math]
Dalej przeprowadzimy dowód przez rozważenie przypadków.
Jeżeli [math]a=b[/math], to [math]\left( a,b\right)=\left( a,a\right)=\left\{ \left\{ a\right\} \right\}[/math], zatem [math]\left( a,d\right)=\left( a,b\right)=\left\{ \left\{ a\right\} \right\}[/math], więc ponieważ [math]\left( a,d\right)=\left\{ \left\{ a\right\},\left\{ a,d\right\} \right\} =\left\{ \left\{ a\right\} \right\}[/math], to z zasady równości zbiorów [math]\left\{ a,d\right\} \in \left\{ \left\{ a\right\} \right\}[/math], a więc [math]\left\{ a,d\right\}=\left\{ a\right\}[/math] , i dalej podobnie [math]d=a=b[/math], czyli [math]d=b[/math], co należało pokazać.
W przeciwnym przypadku, gdy [math]a \neq b[/math], to wtedy [math]\left( a,b\right)=\left\{ \left\{ a\right\},\left\{ a,b\right\} \right\}=\left( a,d\right)=\left\{ \left\{ a\right\},\left\{ a,d\right\} \right\}[/math]. Ponieważ [math]\left\{ a,b\right\} \in \left\{ \left\{ a\right\},\left\{ a,b\right\} \right\}[/math], więc [math]\left\{ a,b\right\} \in \left( a,d\right)=\left\{ \left\{ a\right\},\left\{ a,d\right\} \right\}[/math]. Daje to dwie możliwości: albo [math]\left\{ a,b\right\}=\left\{ a\right\}[/math], co prowadzi do [math]b=a[/math]-sprzeczność. Musi więc zajść drugi przypadek [math]\left\{ a,b\right\} =\left\{ a,d\right\}[/math], co daje [math]b\in \left\{ a,d\right\}[/math], i ponieważ [math]b \neq a[/math] to [math]b=d[/math], co należało pokazać.
Dowód [math]\Longleftarrow[/math] jest oczywisty, teza wynika wprost z założeń i zasady równości zbiorów.[math]\square[/math]
Ćwiczenie 2. Dla każdej pary uporządkowanej [math]x=\left( a,b\right)[/math], udowodnij, że [math]\bigcap\bigcap x=a.[/math]
To ćwiczenie ma bardziej charakter formalny. Przypomnijmy bowiem, że jedynymi przez nas rozważanymi obiektami (bytami) są zbiory. Wobec czego para uporządkowana [math]x=\left( a,b\right)[/math] jest zbiorem ( patrz definicja na początku tego rozdziału), jest to zbiór złożony ze zbiorów, bo elementy zbiorów są również zbiorami, więc możemy utworzyć iloczyn rodziny [math]x=\left( a,b\right)[/math], otrzymując zbiór [math]\bigcap x[/math]- znowu zbiór złożony ze zbiorów, i wtedy iloczyn takiej rodziny zbiorów [math]\bigcap\mathbb{A}[/math], gdzie [math]\mathbb{A}=\bigcap x[/math] ma być równe zbiorowi [math]a[/math] ( współrzędne par uporządkowanych są również zbiorami).
Rozwiązanie: [math]\bigcap \left(x=\left( a,b\right) =\left\{ \left\{ a\right\},\left\{ a,b\right\} \right\}\right)=\bigcap\left\{ \left\{ a\right\},\left\{ a,b\right\} \right\}=\left\{ a\right\} \cap \left\{ a,b\right\}=\left\{ a\right\}.[/math]
Zatem [math]\bigcap\bigcap x=\bigcap\left\{ a\right\}=a.[/math]
Pojęcie pary uporządkowanej jest potrzebne do wprowadzenia iloczynu kartezjańskiego, a potem relacji.
Iloczyn kartezjański
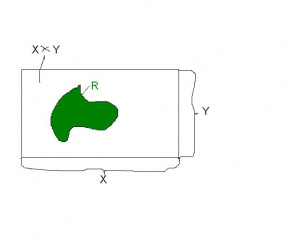
Iloczynem kartezjańskim zbiorów [math]X,Y[/math], to zbiór [math] X\times Y=\left\{\left( x,y\right)\Bigl| \ x\in X, y\in Y\right\}.[/math]
Czyli jest to zbiór wszystkich par uporządkowanych elementów kolejnych zbiorów [math]X,Y[/math]. Np. [math]\left( 1,2\right) ,\left( 2,2\right),\left( 2,1\right) \in \left[ 0,2\right] \times \left[ 1,2\right].[/math] Graficzną ilustracją iloczynu kartezjańskiego jest prostokąt- zobacz ilustracje obok. Na ogół [math]X\times Y\neq Y\times X[/math]- aby się o tym przekonać wyznacz np. [math]\left[ 0,1\right] \times \left[ 0,2\right][/math] i [math]\left[ 0,2\right] \times \left[ 0,1\right].[/math]
Podstawowe własności iloczynu kartezjańskiego:
Twierdzenie 1.1. Dla dowolnych zbiorów [math]X,Y,Z[/math]:
[math]1. \ X\times\left\{ \right\} =\left\{ \right\} =\left\{ \right\} \times X. \\
2. \ X\times\left( Y\cup Z\right)=\left( X\times Y\right) \cup \left( X\times Z\right), \ \ \left( X\cup Y\right)\times Z=\left( X\times Z\right) \cup \left( Y\times Z\right). \\
3. \ X\times\left( Y\cap Z\right)=\left( X\times Y\right) \cap \left( X\times Z\right). \\
4. \ X\times\left( Y\setminus Z\right)=\left( X\times Y\right) \setminus \left( X\times Z\right). [/math]
Dowód:
1. Nie wprost. Gdyby iloczyn kartezjański [math]X\times\left\{ \right\}[/math] byłby niepusty, to istniałaby para [math]\left( x,a\right) \in X\times\left\{ \right\}[/math], a więc wtedy [math]x\in X[/math] i [math]a\in\left\{ \right\}[/math], a zbiór pusty nie posiada elementów, a [math]a[/math] świadczy o tym, że posiada- sprzeczność. Dowód drugiej równości jest analogiczny. [math]\square[/math]
Nim przejdziemy do dalszych dowodów. potrzebny będzie nam następujący prosty fakt: dla dowolnych [math]a,b[/math] oraz dowolnych zbiorów [math]A,B[/math], mamy:
[math]\left( a,b\right) \in A\times B \Longleftrightarrow a\in A \wedge b\in B.[/math]
Wynika to z definicji iloczynu kartezjańskiego. Jedyne, co wymaga krótkiego uzasadnienia, to wynikanie [math]\Longrightarrow.[/math]
Jeżeli [math]\left( a,b\right) \in A\times B [/math], to [math]\left( a,b\right)=\left( c,d\right)[/math], gdzie [math]c\in A, d\in B[/math]. Wtedy jednak z twierdzenia 1, mamy [math]a=c\in A[/math] i [math]b=d\in B[/math], czyli [math]a\in A[/math] i [math]b\in B[/math].
Przechodzimy do dowodu punktu 2.
Ponieważ obydwa zbiory są zbiorami par uporządkowanych, więc wykażemy, że dowolna para należy do jednego zbioru wtedy i tylko wtedy, gdy należy do drugiego. Weźmy dowolną parę [math]\left( a,b\right)[/math], wtedy na podstawie wprowadzonej własności i definicji sumy dwóch zbiorów:
[math] (a,b)\in X \times (Y \cup Z) \Leftrightarrow\\ a \in X \wedge b\in (Y\cup Z) \Leftrightarrow\\ a\in X \wedge (b\in Y \vee b\in Z) \Leftrightarrow\\ (a\in X \wedge b\in Y) \vee (a\in X \wedge b\in Z) \Leftrightarrow\\ (a,b) \in X \times Y \vee (a,b)\in X \times Z \Leftrightarrow\\ (a,b) \in \left( X\times Y\right) \cup \left( X\times Z\right). [/math]
Zatem, (patrz komentarz początek) [math]X\times\left( Y\cup Z\right)=\left( X\times Y\right) \cup \left( X\times Z\right).[/math] Dowód drugiej równości jest analogiczny. [math]\square[/math]
3. Ponieważ obydwa zbiory są zbiorami par uporządkowanych, więc znowu wykażemy, że dowolna para należy do jednego zbioru wtedy i tylko wtedy, gdy należy do drugiego. Weźmy dowolną parę [math](a,b)[/math], wtedy:
[math] (a,b)\in X \times (Y \cap Z) \Leftrightarrow\\ a \in X \wedge b\in (Y\cap Z) \Leftrightarrow\\ a\in X \wedge (b\in Y \wedge b\in Z) \Leftrightarrow\\ (a\in X \wedge b\in Y) \wedge (a\in X \wedge b\in Z) \Leftrightarrow\\ (a,b) \in X \times Y \wedge (a,b)\in X \times Z \Leftrightarrow\\ (a,b) \in \left( X\times Y\right) \cap \left( X\times Z\right),[/math]
co należało otrzymać.
4. Na tej samej zasadzie co poprzednio, weźmy dowolną parę [math](a,b)[/math]. Wtedy:
[math] (a,b) \in (X \times Y) \setminus (X \times Z) \Leftrightarrow (a,b) \in (X \times Y)\wedge (a,b) \notin (X \times Z)\Leftrightarrow \\ a\in X \wedge b\in Y \wedge \neg(a\in X \wedge b\in Z) \Leftrightarrow\\ b\in Y \wedge (a\in X \wedge (a\notin X \vee b\notin Z)) \Leftrightarrow\\ b\in Y \wedge [(a\in X \wedge a\notin X) \vee (a\in X \wedge b\notin Z)] \Leftrightarrow\\ b\in Y \wedge (a\in X \wedge b\notin Z) \Leftrightarrow a\in X \wedge (b\in Y\wedge b\notin Z)\Leftrightarrow\\ a\in X \wedge (b\in Y \setminus Z) \Leftrightarrow (a,b) \in X \times (Y \setminus Z), [/math]
co należało otrzymać. Dowód jest zakończony. [math]\square[/math]
Fakt 1.2. Dla dowolnych zbiorów [math]A,B,C,D[/math], mamy:
[math]A\subset B \wedge C\subset D \Longrightarrow A\times C\subset B\times D.[/math]
Czyli jeden iloczyn kartezjański [math]A\times C[/math] będzie się zawierać w drugim iloczynie kartezjańskim [math]B\times D[/math], jeśli tylko ten mniejszy (pod względem inkluzji) iloczyn kartezjański ma mniejsze odpowiednie składowe- czyli gdy zbiór [math]A[/math] mniejszy jest od [math]B[/math], i [math]C[/math] mniejszy jest od [math]D[/math]- to wtedy iloczyn kartezjański mniejszych zbiorów jest mniejszy od odpowiedniego mu iloczynu kartezjańskiego większych zbiorów (mniejszy,większy należy rozumieć jako słabo mniejszy,słabo większy- dopuszczamy równość zbiorów).
Dowód: Zakładamy, że [math]A\subset B[/math] i [math]C\subset D[/math], chcemy pokazać, że [math]A\times C\subset B\times D.[/math] Niech [math]\left( x,y\right)\in A\times C.[/math] Zatem [math]x[/math] należy do zbioru [math]A[/math], [math]y[/math] należy do [math]C[/math]. Ponieważ z założenia [math]A\subset B[/math], to [math]x[/math] należy do [math]B[/math]. Podobnie, ponieważ [math]C\subset D[/math], to [math]y[/math] należy do [math]D[/math]. Z tych dwóch ostatnich wniosków otrzymujemy, że [math]\left( x,y\right)\in B\times D.[/math] Zatem [math]A\times C\subset B\times D.\square[/math]
Szczególnym przypadkiem powyższego twierdzenia, jest fakt, że dla dowolnych zbiorów [math]A,B,C[/math], mamy:
[math]A\subset B \Longrightarrow A\times C\subset B\times C.[/math]
Aby to udowodnić, weźmy dowolne zbiory [math]A,B,C[/math], takie, że [math]A\subset B[/math]. Stosujemy ten Fakt 1.2. do tych samych zbiorów, i zbioru [math]D=C[/math]. Ponieważ mamy, że [math]A\subset B[/math], i [math]C\subset D=C[/math], to stosując ten fakt dostajemy, że [math]A\times C\subset B\times C.\square[/math]
Podobnie szczególnym przypadkiem tego Faktu 1.2., jest fakt, że dla dowolnych zbiorów [math]A,B,C[/math], mamy:
[math]A\subset B \Longrightarrow C\times A\subset C\times B.[/math]
Dokładana konstrukcja iloczynu kartezjańskiego została omówiona w dodatku dla dociekliwych Dla dociekliwych, gdzie została przedstawiona konstrukcja zgodna z aksjomatem wycinania.
Nim przejdziemy dalej do tematu relacji odnotujmy jeszcze zapomniane dwa proste fakty. Pierwszy mówi, że dla dowolnych zbiorów [math]A,B.C,D,[/math] mamy:
[math]A\subset B \wedge C\subset D \Longrightarrow A\cup C\subset B\cup D.[/math]
Czyli, że suma większych zbiorów (pod względem inkluzji) jest większa. Prosty dowód (trzeba tylko rozważyć dwa przypadki ze względu na przynależność do sumy) pozostawiamy czytelnikowi.
Drugi prosty fakt jest podobny- dotyczy tylko iloczynu. Dla dowolnych zbiorów [math]A,B.C,D,[/math] mamy:
[math]A\subset B \wedge C\subset D \Longrightarrow A\cap C\subset B\cap D.[/math]
Czyli iloczyn większych zbiorów jest większy. Dowód czytelnikowi nie nastręczy trudności.
Relacje
Podstawowym pojęciem (i fundamentalnym) teorii mnogości jest pojęcie relacji.
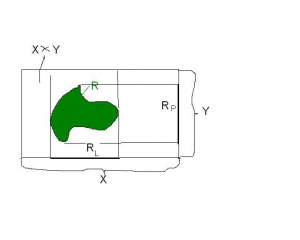
Niech [math]X,Y[/math] będą zbiorami. Relacją między zbiorami [math]X[/math] a [math]Y[/math], nazywamy każdy podzbiór [math]R\subset X\times Y.[/math]
Czyli tworzymy najpierw iloczyn kartezjański [math]X\times Y[/math], każdy podzbiór tego zbioru to przykład relacji między [math]X[/math] a [math]Y[/math]. Zobacz ilustrację obok.
Ważne relacje:
[math]\emptyset-[/math] relacja pusta( zbiór pusty jest podzbiorem każdego zbioru).
[math]X\times Y[/math]- relacja pełna (każdy zbiór jest podzbiorem swoim własnym, więc również spełnia to iloczyn [math]X\times Y[/math]).
Relacją w zbiorze [math]X[/math] , nazywamy każdy podzbiór [math]R\subset X\times X.[/math]
Przykładem znowu może być relacja pusta, relacja totalna [math]X\times X[/math], ale również:
[math]I_{X}=\left\{ \left( x,y\right) \in X\times X\Bigl| \ \ x=y\right\}.[/math] Relacja identyczności- dwa elementy są w relacji gdy są identyczne, równe.
Gdy [math]\left( x,y\right) \in R[/math], gdzie [math]x\in X, y\in Y[/math], to mówimy, że elementy [math]x,y[/math] są ze sobą w relacji [math]R[/math]. Zapisujemy to też jako: [math]x(R)y[/math]. Też dla innych oznaczeń relacji- jeśli oznaczymy relację przez np. [math]\sim[/math], to fakt, że elementy [math]x,y[/math] są ze sobą w relacji [math]\sim[/math], zapiszemy jako: [math]x\sim y[/math].
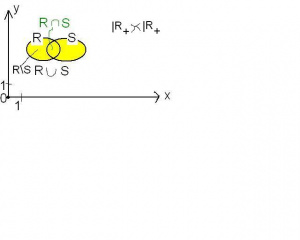
Suma, iloczyn i różnica relacji
Na relacjach można wykonywać działania mnogościowe. I tak, dla relacji [math]R,S\subset X\times Y,[/math] relacja [math]R\cup S[/math], to taka relacja, że dwa elementy [math]x,y[/math] są ze sobą w relacji [math]R\cup S[/math], jeśli tylko są ze sobą w relacji [math]R[/math], oraz wtedy, jeśli tylko są ze sobą w relacji [math]S[/math]. Czyli [math]\left( x,y\right) \in R\cup S\Longleftrightarrow \left( x,y\right) \in R\vee \left( x,y\right) \in S[/math].
Podobnie, dla relacji [math]R,S\subset X\times Y,[/math] relacja [math]R\cap S[/math], to taka relacja, że dwa elementy [math]x,y[/math] są ze sobą w relacji [math]R\cap S[/math], jeśli są ze sobą w relacji [math]R[/math], oraz równocześnie są ze sobą w relacji [math]S[/math]. Czyli [math]\left( x,y\right) \in R\cap S\Longleftrightarrow \left( x,y\right) \in R\wedge \left( x,y\right) \in S.[/math]
Podobnie, różnica relacji [math]R,S[/math]- relacja [math]R\setminus S[/math], to taka relacja, że dwa elementy są ze sobą w relacji [math]R\setminus S[/math], gdy są ze sobą w relacji [math]R[/math] i nie są ze sobą w relacji [math]S[/math], tzn. [math]\left( x,y\right) \in R\setminus S\Longleftrightarrow \left( x,y\right) \in R\wedge \left( x,y\right) \not\in S.[/math]
Ilustracja tych operacji jest podobna do ilustracji działań mnogościowych na zbiorach- zobacz ilustrację obok. Różnica polega na tym, że mamy wprowadzoną strukturę iloczynu kartezjańskiego, i na punkty patrzymy nie na jako zwykłe elementy, tylko jak na pary uporządkowane.
Co więcej, niech [math]\mathbb{A}[/math] będzie pewną rodziną relacji z [math]X[/math] do [math]Y[/math]. Wtedy [math]\bigcup \mathbb{A}[/math]- suma rodziny relacji z [math]X[/math] do [math]Y[/math], a więc suma rodziny podzbiorów [math]X\times Y[/math] jest podzbiorem [math]X\times Y[/math], a więc jest relacją z [math]X[/math] do [math]Y[/math]. Stąd mamy ważne:
Twierdzenie 2.1. Suma dowolnej rodziny relacji z [math]X[/math] do [math]Y[/math] jest relacją z [math]X[/math] do [math]Y[/math].
Dla takiej relacji, mamy: [math]\left( x,y\right) \in \bigcup \mathbb{A}\Longleftrightarrow \left( x,y\right) \in R[/math], dla pewnej relacji [math]R\in\mathbb{A}.[/math]
Tzn. dwa elementy są ze sobą w relacji [math]\bigcup \mathbb{A}[/math], gdy są z sobą w relacji [math]R[/math], dla pewnej relacji [math]R[/math] z rodziny relacji [math]\mathbb{A}.[/math]
Podobnie możemy określić iloczyn rodziny relacji. Dla niepustej rodziny [math]\mathbb{A}[/math] relacji z [math]X[/math] do [math]Y[/math], relacja [math]\bigcap \mathbb{A}[/math], to taka relacja, że dwa elementy są ze sobą w relacji [math]\bigcap \mathbb{A}[/math], gdy są z sobą w relacji [math]R[/math], dla każdej relacji [math]R\in\mathbb{A}.[/math]
Określimy podstawowe operacje na relacjach.
Niech [math]R \subset X \times Y.[/math] Lewą dziedziną relacji [math]R[/math] nazywamy zbiór [math]R _{L}:[/math]
[math]R _{L}=\left\{ x\in X\Bigl| \ \ \bigvee\limits_{y\in Y} \left( x,y\right) \in R \right\} \subset X.[/math]
Natomiast prawą dziedziną relacji [math]R[/math] nazywamy zbiór [math]R _{P}:[/math]
[math]R _{P}=\left\{ y\in Y\Bigl| \ \ \bigvee\limits_{x\in X} \left( x,y\right) \in R \right\} \subset Y.[/math]
Zbiór [math]R _{L}[/math]- jest to zbiór tych [math]x[/math]-ów, gdzie jest przynajmniej jeden [math]y[/math], że elementy [math]x,y[/math] są ze sobą w relacji [math]R[/math]. Mówiąc prościej, jest to zbiór lewych współrzędnych par tej relacji [math]R[/math]. Analogicznie, zbiór [math]R _{P}[/math]- jest to zbiór prawych współrzędnych par tej relacji [math]R[/math]. Możemy powiedzieć, że zbiór [math]R _{L}[/math] jest rzutem relacji [math]R[/math] na oś [math]x[/math], a zbiór [math]R _{P}[/math] jest rzutem relacji [math]R[/math] na oś [math]y[/math]. Zobacz ilustrację obok.
Przykład. Niech [math]X=\left\{ 1,2,3\right\}, Y=\left\{ 1,2\right\}, R=\left\{ \left( 1,1\right),\left( 1,2\right),\left( 2,2\right) \right\}.[/math] Wtedy [math]R _{L}=\left\{ 1,2\right\} [/math], [math]R _{P}=\left\{ 1,2\right\}=Y.[/math]
Poniżej podaje prosty, lecz ciekawy fakt:
Fakt 2.2. Dla dowolnej relacji [math]R \subset X \times Y,[/math] mamy: [math]R \subset R _{L} \times R _{P}.[/math]
Dowód:
Niech [math]\left( x,y\right) \in R.[/math] Mamy oczywiście [math]x\in X, y\in Y[/math]. Ponieważ [math]\left( x,y\right) \in R[/math], to [math]x[/math] jest lewą współrzędną pary z relacji [math]R[/math], a więc [math]x\in R _{L}.[/math] Podobnie ponieważ [math]y[/math] jest prawą współrzędną pary z relacji [math]R[/math], to [math]y\in R _{P}[/math]. Ponieważ [math]x\in R _{L}[/math] i [math]y\in R _{P}[/math], to [math]\left( x,y\right) \in R _{L} \times R _{P},[/math] i [math]R \subset R _{L} \times R _{P}.\square[/math]
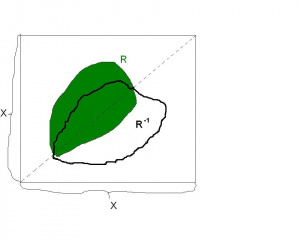
Relacja odwrotna- powstaje poprzez symetrię względem przekątnej
Niech [math]R\subset X\times Y[/math]. Relację odwrotną do relacji [math]R[/math] nazywamy relację [math]R^{-1}\subset Y\times X[/math], określoną jako:
[math]R^{-1}=\left\{ \left( y,x\right) \in Y\times X \Bigl| \ \ \left( x,y\right) \in R \right\}.[/math]
Tzn. element [math]y[/math] jest w relacji z elementem [math]x[/math] w relacji [math]R^{-1}[/math], gdy [math]x[/math] jest w relacji z [math]y[/math]( czyli na odwrót) w relacji [math]R.[/math] Gdy X=Y, to możemy relację odwrotną zilustrować- zobacz obok rysunek.
Przykład. Niech [math]X=\left\{ a,b.c \right\}.[/math] Niech [math]R\subset X\times X[/math], będzie dana jako: [math]R= \left\{ \left( a,a\right),\left( a,b\right),\left( a,c\right),\left( b,b\right)\right\} .[/math] Wtedy [math]R^{-1} = \left\{ \left( a,a\right),\left( b,a\right),\left( c,a\right),\left( b,b\right) \right\}.[/math]
Fakt 2.3. Niech [math]X,Y[/math] będą dowolnymi ustalonymi zbiorami, oraz niech [math]R,S\subset X\times Y[/math] będą dowolnymi relacjami. Pokażemy własności tych relacji:
[math]1. \ \left( R\cup S\right) ^{-1}=R ^{-1} \cup S ^{-1}. \\[/math]
[math]2. \ \left( R\cap S\right) ^{-1}=R ^{-1} \cap S ^{-1}. \\[/math]
[math]3. \ \left( R\setminus S\right) ^{-1}=R ^{-1} \setminus S ^{-1}. \\[/math]
[math]4. \ \left( R^{-1}\right) ^{-1}=R . \\[/math]
Czyli relacją odwrotną do sumy relacji jest suma relacji odwrotnych, podobnie dla iloczynu i różnicy.
Dowód:
Niech [math]x\in X, y\in Y.[/math] Wtedy:
[math]1. \ \ \left( y,x\right) \in \left( R\cup S\right) ^{-1} \Leftrightarrow \left( x,y\right) \in R\cup S \Leftrightarrow \left( x,y\right) \in R \vee \left( x,y\right) \in S \Leftrightarrow \left( y,x\right) \in R ^{-1} \vee \left( y,x\right) \in S ^{-1} \Leftrightarrow \left( y,x\right) \in R ^{-1} \cup S ^{-1}.[/math] Zatem [math]\left( R\cup S\right) ^{-1}=R ^{-1} \cup S ^{-1}.[/math]
2. Dowód jest analogiczny do poprzedniego.
[math]3. \ \ \left( y,x\right) \in \left( R\setminus S\right) ^{-1} \Leftrightarrow \left( x,y\right) \in R\setminus S \Leftrightarrow \left( x,y\right) \in R \wedge \left( x,y\right) \notin S \Leftrightarrow \left( y,x\right) \in R ^{-1} \wedge \left( y,x\right) \notin S ^{-1} \Leftrightarrow \left( y,x\right) \in R ^{-1} \setminus S ^{-1}.[/math] Zatem [math]\left( R\setminus S\right) ^{-1}=R ^{-1} \setminus S ^{-1}.[/math]
[math]4. \ \ \left( x,y\right) \in \left( R^{-1}\right) ^{-1} \Leftrightarrow \left( y,x\right) \in R^{-1} \Leftrightarrow \left( x,y\right) \in R.[/math] Zatem [math]\left( R^{-1}\right) ^{-1}=R .\square[/math]
Na koniec tego podrozdziału wprowadzamy pojęcie relacji zwrotnej.
Relację [math]R \subset X\times X[/math] nazywamy zwrotną, gdy dla dowolnego [math]x\in X[/math] zachodzi [math]\left( x,x\right) \in R.[/math]
Relacja w zbiorze [math]X[/math] jest więc zwrotna, gdy każdy element [math]x\in X[/math] jest w relacji z samym sobą. Przykład: [math]X=\left\{ 0,1\right\}[/math]. Relacja [math]R=\left\{ \left( 0,0\right),\left( 1,1\right) ,\left( 0,1\right) \right\}[/math] jest zwrotna. Inny przykład: [math]X=\left\{ 0,1,2\right\}[/math], relacja [math]R=\left\{ \left( 0,0\right),\left( 1,1\right),\left( 1,2\right) \right\}[/math] nie jest zwrotna, bo [math]\left( 2,2\right) \not\in R.[/math]
Poniżej podaje prosty fakt.
Fakt 2.4. Relacja [math]R \subset X\times X[/math] jest zwrotna, wtedy i tylko wtedy, gdy [math]R \supset I_{X}[/math]. Zobacz ilustrację obok. A więc relacja jest zwrotna, gdy zawiera przekątną- identyczność na zbiorze [math]X[/math].
Dowód: [math]\Longrightarrow[/math] Niech relacja [math]R \subset X\times X[/math] będzie zwrotna. Niech [math]\left( x,y\right) \in I_{X}[/math]. Ponieważ jest to relacja identyczności, to [math]x=y[/math]. A ponieważ [math]R[/math] jest zwrotna, to [math]\left( x,y\right)=\left( x,x\right) \in R.[/math] A więc [math]R \supset I_{X}[/math].
[math]\Longleftarrow[/math] Załóżmy, że [math]R \supset I_{X}[/math]. Niech [math]x\in X.[/math] Wtedy [math]\left( x,x\right) \in I_{X}[/math], a ponieważ [math]R \supset I_{X}[/math], to [math]\left( x,x\right) \in R.[/math] Wobec dowolności [math]x\in X[/math] oznacza to, że [math]R[/math] jest zwrotna.[math]\square[/math]
Domknięcia relacji
Najpierw wprowadźmy pewien termin z rachunku zbiorów.
Niech [math]\mathbb{A}[/math] będzie pewną rodziną (zbiorem ) podzbiorów zbioru [math]X[/math]. Rodzina zbiorów [math]\mathbb{A}[/math] jest zamknięta na przekroje, gdy spełnia:
jeśli [math]\{ \}\neq\mathbb{B}\subset\mathbb{A}[/math], to [math]\bigcap\mathbb{B}\in\mathbb{A}.[/math]
Czyli, gdy mamy dowolny niepusty zbiór [math]\mathbb{B}[/math] zbiorów z rodziny [math]\mathbb{A}[/math], to przekrój takich zbiorów jest również elementem rodziny [math]\mathbb{A}.[/math]
Przykład- będzie on dotyczył relacji. Niech [math]X[/math] będzie dowolnym ustalonym zbiorem. Niech [math]\mathbb{A}=\left\{ R\subset X\times X\Bigl| \ \ R \hbox{ jest zwrotna}\right\}. [/math] Jest to rodzina wszystkich relacji zwrotnych. Wykażemy, że rodzina zbiorów [math]\mathbb{A}[/math] jest zamknięta na przekroje.
Niech [math]\{ \}\neq\mathbb{B}\subset\mathbb{A}.[/math] Pokażemy, że [math]\bigcap\mathbb{B}\in\mathbb{A}[/math] czyli, że przekrój dowolnej niepustej rodziny relacji zwrotnych jest relacją zwrotną.
Niewątpliwie, iloczyn niepustej rodziny relacji z [math]X[/math] do [math]X[/math], jest relacją z [math]X[/math] do [math]X[/math]- stąd [math]\bigcap\mathbb{B}\subset X\times X.[/math] Niech [math]x\in X.[/math] Niech [math]R\in\mathbb{B}.[/math] Ponieważ każda relacja [math]R\in\mathbb{B}[/math] jest zwrotna, więc [math]\left( x,x\right) \in R.[/math] Z własności relacji iloczynu relacji (oraz tego, że rodzina [math]\mathbb{B}[/math] jest niepusta), to [math]\left( x,x\right)\in\bigcap \mathbb{B}.[/math] Zatem [math]\bigcap\mathbb{B}[/math] jest zwrotna, i [math]\bigcap\mathbb{B}\in\mathbb{A}.\square[/math]
Poniżej definiujemy domknięcie relacji.
Niech [math]\mathbb{A}[/math] będzie pewną rodziną (zbiorem ) relacji w zbiorze [math]X[/math]. Niech relacja [math]R\subset X\times X.[/math] Relacja [math]S\subset X\times X[/math] jest domknięciem relacji [math]R[/math], w zbiorze relacji [math]\mathbb{A}[/math], gdy:
[math]1. \ S\supset R, \\
2. \ S\in \mathbb{A}, \\
3. \ \hbox{ jeśli relacja }T \hbox{ spełnia 1. i 2., to } T\supset S, \hbox{ czyli, dla każdej relacji } T,( \hbox{ jeśli }T \supset R \hbox{ oraz } T\in \mathbb{A} \hbox{ to } T\supset S).[/math]
Czyli jeśli mamy ustalony zbiór relacji, to dla relacji(być może spoza zbioru) jej domknięcie to relacja będąca jej nadzbiorem, będąca elementem zbioru relacji, i najmniejsza taka relacja, tzn. jeśli relacja [math]T[/math] spełnia [math]1.[/math] i [math]2.[/math] to [math]T[/math] musi zawierać domknięcie [math]S[/math]. Zatem domknięcie relacji, jest to najmniejsza relacja( pod względem inkluzji, zawierania) zawierająca daną relację [math]R[/math] należąca do zbioru relacji [math]\mathbb{A}.[/math]
Następny lemat mówi, że domknięcie relacji jeżeli istnieje to jest jedyne.
Lemat 3.1. Jeśli [math]\mathbb{A}[/math] jest dowolnym zbiorem relacji w zbiorze [math]X[/math], [math]R[/math] jest dowolną relacją w zbiorze [math]X[/math], oraz istnieją domknięcia [math]S_1,S_2[/math] relacji [math]R[/math], to wtedy [math]S_1=S_2.[/math]
Czyli istnieje tylko jedno domknięcie relacji [math]R[/math].
Dowód:
Przypuśćmy, że [math]S_1,S_2[/math] są domknięciami relacji [math]R[/math]. Pokażemy, że [math]S_1=S_2.[/math] Ponieważ [math]S_1[/math] jest domknięciem relacji [math]R[/math], to [math]S_1\supset R, S_1\in \mathbb{A}[/math], i [math]S_1[/math] jest najmniejszą relacją o tych własnościach. Podobnie, ponieważ [math]S_2[/math] jest domknięciem relacji [math]R[/math], to [math]S_2\supset R[/math], [math]S_2\in \mathbb{A}[/math], i [math]S_2[/math] jest najmniejszą relacją o tych własnościach. Stosując zatem punkt 3, do domknięcia [math]S_1[/math], i relacji [math]T=S_2[/math] otrzymujemy, że [math]S_2\supset S_1.[/math] W sposób symetryczny uzasadniamy, że [math]S_1\supset S_2.[/math] Zatem [math]S_1=S_2.\square[/math]
Poniższe twierdzenie dostarcza warunku, przy którym takie domykanie relacji jest zawsze możliwe.
Twierdzenie 3.2. Niech [math]\mathbb{A}[/math] będzie dowolnym zbiorem relacji w zbiorze [math]X[/math]. Wtedy poniższe dwa warunki są równoważne.
1. Rodzina [math]\mathbb{A}[/math] jest zamknięta na przekroje i [math]X\times X \in \mathbb{A}.[/math]
2. Każda relacja ma domknięcie w zbiorze relacji [math]\mathbb{A}.[/math]
Dowód:
[math](1) \rightarrow (2).[/math] Niech [math]R[/math] będzie relacją w zbiorze [math]X[/math]. Utwórzmy zbiór relacji jako: [math]\mathbb{B}= \left\{ S\subset X \times X\Bigl | \ \ R\subset S \wedge S \in \mathbb{A}\right\} .[/math] Ponieważ z założenia [math](1)[/math], mamy [math]X\times X \in \mathbb{A}[/math], więc łatwo sprawdzić, że [math]X\times X \in \mathbb{B}.[/math] Zatem rodzina [math]\mathbb{B}[/math] jest niepusta. Pokażemy, że [math]\bigcap \mathbb{B}[/math] jest domknięciem relacji [math]R[/math], w zbiorze relacji [math]\mathbb{A}.[/math] Z określenia rodziny [math]\mathbb{B}[/math] wynika, że relacja [math]R[/math] zawiera się w każdej relacji tej rodziny, zatem również [math]R[/math] zawiera się w ich iloczynie, a więc [math]R\subset \bigcap \mathbb{B}[/math]. Ponieważ z określenia rodziny [math]\mathbb{B}[/math] wynika, że każdy jej element jest elementem [math]\mathbb{A}[/math], to na podstawie [math](1)[/math]otrzymujemy, że również [math]\bigcap \mathbb{B} \in \mathbb{A}.[/math] Minimalność [math]\bigcap \mathbb{B}[/math] uzasadniamy przez: niech relacja [math]T \supset R[/math], będzie taka, że [math]T\in\mathbb{A}.[/math] Oznacza to, że [math]T\in\mathbb{B}.[/math] Zatem z własności iloczynu [math]\bigcap \mathbb{B}\subset T.[/math] W ten oto sposób zostały spełnione wszystkie wymagania stawiane relacji [math]\bigcap \mathbb{B}[/math] na bycie domknięciem relacji [math]R[/math] w zbiorze relacji [math]\mathbb{A}[/math], a więc relacja [math]R[/math] ma domknięcie w zbiorze relacji [math]\mathbb{A}.[/math]
[math](2) \rightarrow (1).[/math] Na początek zauważmy, że relacja [math]X\times X[/math] (jak każda) ma domknięcie w zbiorze relacji [math]\mathbb{A}.[/math] Domknięcie takie musi być nadzbiorem relacji i elementem zbioru [math]\mathbb{A}.[/math] A ponieważ domknięcie nie może być istotnym nadzbiorem [math]X\times X[/math], więc musi być równe [math]X\times X[/math], stąd [math]X\times X \in \mathbb{A}.[/math] Niech [math]\left\{ \right\} \neq \mathbb{B} \subset \mathbb{A}.[/math] Pokażemy, że [math]\bigcap \mathbb{B} \in \mathbb{A}.[/math] Niewątpliwie iloczyn niepustej rodziny relacji z [math]X[/math]do [math]X[/math] jest relacją z [math]X[/math] do [math]X[/math]. Relacja ta ([math]\bigcap \mathbb{B}[/math]) ma domknięcie w zbiorze relacji [math]\mathbb{A},[/math] nazwijmy je [math]S[/math]. Punkt [math](3)[/math] definicji domknięcia mówi, że dla dowolnej relacji [math]T[/math], o ile [math]\bigcap \mathbb{B} \subset T[/math] i [math]T\in \mathbb{A}[/math] to [math]S \subset T.[/math] Połóżmy za [math]T[/math] dowolny element z [math]\mathbb{B}.[/math] Założenia implikacji pozostają spełnione, jest więc tak, że [math]S \subset T[/math], dla dowolnej relacji [math]T\in\mathbb{B}.[/math] W takim razie z własności iloczynu [math]S \subset \bigcap \mathbb{B}[/math]. Ponieważ mamy też [math]\bigcap \mathbb{B} \subset S[/math], bo [math]S[/math] jest domknięciem [math]\bigcap \mathbb{B},[/math] jest więc [math]\bigcap \mathbb{B}= S[/math], a ponieważ domknięcie [math]S[/math] relacji [math]\bigcap \mathbb{B}[/math] w zbiorze relacji [math]\mathbb{A},[/math] jest elementem [math]\mathbb{A},[/math] to [math]\bigcap \mathbb{B} \in \mathbb{A}[/math]. Zatem rodzina [math]\mathbb{A}[/math] jest zamknięta na przekroje i [math]X\times X \in \mathbb{A}.\square[/math]
Jako przykład zastosowania tego twierdzenia rozważmy zbiór [math]X[/math], i rodzinę [math]\mathbb{A}[/math] wszystkich relacji zwrotnych w zbiorze [math]X[/math]. Wykazaliśmy już na początku tego rozdziału, że taka rodzina jest zamknięta na przekroje. Niewątpliwie relacja [math]X\times X[/math] jest zwrotna, Zatem [math]X\times X\in\mathbb{A}[/math]. Zatem w myśl udowodnionego twierdzenia, każda relacja w zbiorze [math]X[/math] ma domknięcie w zbiorze relacji zwrotnych. Czyli każda relacja w zbiorze [math]X[/math] ma zwrotne domknięcie. Tym domknięciem dla relacji [math]R[/math] jest [math]R\cup I_X.[/math] Pokażemy, że spełnia warunki domknięcia.
1. Niewątpliwie [math]R \subset R\cup I_X.[/math]
2. Również [math]I_X\subset R\cup I_X.[/math] Ponieważ [math]R\cup I_X[/math] zawiera relację identyczności, jest więc zwrotna, a więc [math]\left( R\cup I_X \right) \in\mathbb{A}.[/math]
3. Weźmy dowolną relację [math]T[/math] w zbiorze [math]X[/math], która jest zwrotna, i dla której [math]T\supset R.[/math] Pokażemy, że [math]T\supset R\cup I_X.[/math] Ponieważ [math]T[/math] jest zwrotna, to [math]T\supset I_X.[/math] Ponieważ [math]T\supset I_X[/math] i [math]T\supset R[/math], to [math]T\supset R\cup I_X.[/math]
Wobec czego [math]R\cup I_X[/math] spełnia warunki na bycie domknięciem relacji [math]R[/math], a więc jest domknięciem zwrotnym relacji [math]R[/math] ( domknięcie jest tylko jedno).
Jak widać dodaliśmy do relacji [math]R[/math] relację identyczności. Mówiąc bardziej wymowniej relację [math]R[/math] uzupełniamy o brakujące elementy na przekątnej- wtedy już będzie zwrotna. Czyli relację [math]R[/math] powiększamy (domykamy) tak aby była zwrotna- uzupełniając o brakujące elementy na przekątnej. Podobnie w ogólności, jeśli mamy ustalony zbiór relacji, to relację (być może spoza zbioru) powiększamy (domykamy) tak aby otrzymane domknięcie już było elementem naszego zbioru relacji.