Aksjomaty teorii mnogości
Aksjomatyczna teoria mnogości powstała jako odpowiedź na paradoksy powstające w teorii naiwnej. Poza tym dzięki temu pojęcie zbioru jest bardziej ścisłe. Słowo aksjomat, z greckiego pochodzenia oznacza tezę, która jest oczywista i nie potrzebuję dowodu. Aksjomaty teorii mnogości, to podstawowe prawdy odnośnie zbiorów, a także podstawy naszej teorii- przyjmujemy je bez dowodów, i w oparciu o nie wyprowadzamy bardziej złożone fakty.
Zakładamy, że istnieje jakiś zbiór, chociaż jeden. Zakładamy, że jedynymi rozważanymi obiektami są zbiory. To może wydawać się dziwne ( bo przecież w matematyce są punkty chociażby, i inne obiekty); ale przekonamy się, że wszystkie te podstawowe obiekty matematyczne dadzą się przedstawić jako zbiory. Po co? Gdybyśmy rozważali obiekty niebędące zbiorami ( tzw. urelementy), to zbiory mogłyby być tworzone z tych urelementów, ale również ze zbiorów. Wtedy wypowiedź: jest dowolnym zbiorem- byłaby mniej precyzyjna. A tak, dowolny zbiór- jest to dowolny obiekt naszej teorii, i jest to ścisłe. Zauważmy, że to nasze założenie oznacza, że elementy zbiorów, są również zbiorami. Później może napiszę o klasach, będą to skupiska zbiorów( znowu), tak duże, że nie tworzą zbioru, nazwiemy je klasami. Tak, w aksjomatycznej teorii mnogości już nie każda kolekcja elementów (zbiorów) jest zbiorem- np. nie istnieje zbiór wszystkich zbiorów.
Także dowolny , jest to dowolny byt naszej teorii, zgodnie z powyższym, jest to też dowolny zbiór, ale jest to też rodzina zbiorów- bo, ponieważ jedynymi rozważanymi obiektami są zbiory, więc elementy zbiorów, są także zbiorami, a więc zbiór może być traktowany jako rodzina zbiorów. Niemniej, zawsze będziemy tak pisać, jaka jest istota rzeczy w danym momencie- choć formalnie jest to dowolny , i tym samym zbiór.
Najpierw podajmy aksjomaty związane z równością.
Zakładamy aksjomaty:
I przede wszystkim
Dla dowolnych , oraz dowolnego zbioru , zakładamy, że:
.
Ostatni aksjomat mówi, że jeśli element jest elementem zbioru , to ten sam element (), również jest elementem zbioru .
Przechodzimy do aksjomatów bardziej mnogościowych. Najpierw podamy aksjomat równości zbiorów.
Spis treści
Aksjomat równości zbiorów:
Zakładamy, że następująca formuła jest prawdą:
.
Czyli dwa zbiory są równe (takie same), gdy dla dowolnego elementu - jest w , dokładnie wtedy,. gdy jest w , czyli gdy zbiory mają takie same elementy. Podobnie definiujemy zawieranie, czyli inkluzję zbiorów:
.
Czyli zbiór zawiera się w zbiorze , gdy każdy element zbioru jest elementem zbioru . Mówimy wtedy też, że jest podzbiorem . Jeśli zbiór jest podzbiorem zbioru , oraz te zbiory są różne, to zbiór nazywamy podzbiorem właściwym (istotnym) zbioru . Zapisujemy to jako: , tzn.
Możemy też zdefiniować:
.
Czyli zbiór jest nadzbiorem zbioru , gdy jest podzbiorem .
Poniższe twierdzenie mówi, że dwa zbiory są równe, gdy pierwszy z nich jest podzbiorem drugiego, a drugi jest podzbiorem pierwszego.
Twierdzenie 1.1
Dla dowolnych zbiorów mamy: .
Dowód: Niech będą dowolnymi zbiorami. Wtedy:
Słowami: jeśli i , to każdy element jest elementem ; i każdy element jest elementem ; czyli zbiory mają takie same elementy, a więc są równe.
Następne twierdzenie mówi o przechodniości inkluzji.
Twierdzenie 1.2.
Dla dowolnych zbiorów , mamy: .
Bardzo prosty dowód:
Niech będą dowolnymi zbiorami, takimi, że i . Pokażemy, że . Niech . Wtedy ,( bo ), i dalej , (bo ). Wobec dowolności wyboru elementu , oznacza to, że .
Mówiliśmy, że elementy zbiorów są także zbiorami. Ktoś mógłby zapytać- jakimi zbiorami? Złożonymi z czego? Odpowiedź jest taka: podstawowym startowym zbiorem jest zbiór nieposiadający elementów , zwany zbiorem pustym. A potem tworzymy zbiór - zbiór jednoelementowy złożony ze zbioru pustego, zbiór różny od zbioru pustego( bo zbiór pusty nie ma elementów, a zbiór ma jeden element-). Potem możemy utworzyć - zbiór jednoelementowy złożony z poprzedniego elementu. I w podobny sposób będziemy postępować (to się wydaje niewiarygodne) ale- zbudujemy w ten sposób uniwersum zbiorów, wszystkie te podstawowe pojęcia matematyczne spróbujemy zapisać za pomocą tego typu zbiorów. Nie będzie to łatwym zadaniem, ale za to fascynującym.
Następny aksjomat gwarantuje istnienie zbioru pustego.
Aksjomat zbioru pustego:
Zakładamy, że następująca wypowiedź, zwana aksjomatem zbioru pustego, jest prawdziwa:
Istnieje zbiór nie posiadający elementów, tzn. taki zbiór , że: dla dowolnego :
Każdy taki zbiór nazywamy zbiorem pustym. Aksjomat zbioru pustego mówi więc, że istnieje taki zbiór pusty bez elementów. Teraz pokażemy, że istnieje co najwyżej jeden zbiór pusty, czyli:
Twierdzenie 2.1.
Dowolne dwa zbiory puste są równe.
Dowód: Weźmy dwa zbiory puste, i pokażmy, że są równe. Dwa zbiory są równe, jeśli dowolny element należy do obu z nich równocześnie, albo do żadnego z tych dwóch zbiorów. Weźmy dowolny element . Element ten nie należy do pierwszego zbioru, ( bo jest on pusty), i ten nie należy do drugiego zbioru, ( bo on też jest pusty). Z dowolności wyboru elementu , wnioskujemy, że zbiory są równe.
Aksjomat zbioru pustego głosi, że istnieje co najmniej jeden zbiór pusty. My pokazaliśmy, że dowolne dwa zbiory puste są równe, w związku z czym zbiór pusty jest dokładnie jeden. Oznaczamy go , lub czasem dla czytelności .
Kolejny fakt mówi, że zbiór pusty jest podzbiorem dowolnego zbioru, tzn.:
Fakt 2.2. Dla dowolnego zbioru , mamy: .
Dowód: Weźmy dowolny zbiór . Zgodnie z definicją inkluzji na zbiorach, należy pokazać, że:
.
Ale dla dowolnego ustalonego , warunek jest fałszem, wobec czego cała implikacja jest prawdziwa. Z dowolności wyboru oznacza to, że , co należało pokazać.
Podobnie można uzasadnić, że:
Fakt 2.3. Dla dowolnego zbioru , mamy: .
Czyli, że każdy zbiór jest podzbiorem swoim własnym. Mówimy wtedy, że zbiór jest podzbiorem niewłaściwym (nieistotnym) samego siebie. Bardzo prosty dowód tego faktu, pozostawimy czytelnikowi.
Następny aksjomat gwarantuje istnienie zbiorów jedno- i dwuelementowych.
Aksjomat pary:
Zakładamy, że poniższa wypowiedź, zwana aksjomatem pary, jest prawdą:
Dla dowolnych , istnieje zbiór , tzn. zbiór którego elementami są dokładnie i .
Dla dowolnych , a więc gdy mamy dwa elementy , to istnieje zbiór , a więc możemy utworzyć zbiór . Aksjomat ten mówi więc, że jeśli mamy dwa elementy i , to możemy utworzyć zbiór . W przypadku, gdy , zbiór oznaczamy jako (zbiór ma jeden element- ).
Wniosek 3.1. - istnieje 'nieskończenie' wiele zbiorów.
Wiemy, że istnieje zbiór pusty- jest to dokładnie jeden zbiór, nieposiadający elementów, oznaczmy go tym razem . Na mocy aksjomatu pary możemy skonstruować zbiór jednoelementowy , różny od zbioru pustego. Możemy zastosować ten pomysł jeszcze raz, i utworzyć - zbiór jednoelementowy złożony z poprzedniego zbioru, jako elementu. Przy czym, to jest zbiór różny od poprzednich zbiorów. Tą operacje można powtarzać dowolną ilość razy, tworząc 'nieskończoną' ilość zbiorów. Przy czym, już te same zbiory, nie są więcej niż jednoelementowe.
Następny aksjomat pozwala utworzyć sumę dwóch zbiorów.
Aksjomat sumy dwóch zbiorów:
Zakładamy, że poniższa wypowiedź jest prawdziwa:
Dla dowolnych zbiorów , istnieje zbiór , tzn. zbiór którego elementami są dokładnie wszystkie elementy zbioru , oraz wszystkie elementy zbioru .
Dla dowolnych zbiorów , a więc gdy mamy dwa zbiory , to istnieje zbiór , a więc możemy utworzyć zbiór - sumę mnogościową zbiorów i . Aksjomat ten mówi więc, że dla dwóch zbiorów, możemy utworzyć ich sumę mnogościową.
Ćwiczenie 4.0. Wykaż, przy pomocy aksjomatu sumy dwóch zbiorów, że poniższa wypowiedź jest równoważna aksjomatowi pary: Dla dowolnego istnieje zbiór jednoelementowy .
Rozwiązanie: To, że z aksjomatu pary, wynika powyższa wypowiedź już w zasadzie pokazaliśmy- wystarczy wziąć dowolne , i na mocy aksjomatu pary utworzyć - a więc prawdziwa jest powyższa wypowiedź.
Pokażemy teraz, że z powyższej wypowiedzi wynika aksjomat pary. Aby to pokazać, ustalmy dowolne . Na mocy zakładanej wypowiedzi, dla możemy utworzyć , a dla możemy utworzyć . Korzystając z aksjomatu sumy dwóch zbiorów, możemy utworzyć czyli dokładnie ten sam zbiór, o którym mówi aksjomat pary. Pokazaliśmy aksjomat pary, co kończy dowód implikacji, i całego ćwiczenia.
Kolejny wniosek. to:
Wniosek 4.1.- istnieją dowolne zbiory skończone.
Na podstawie aksjomatu zbioru pustego istnieje zbiór zeroelementowy, na podstawie aksjomatu pary istnieje dowolny zbiór jedno- i dwuelementowy. Aby wykazać, że dla dowolnych . istnieje zbiór , zbiór ten definiujemy jako: . Skoro mamy dowolny zbiór 3-elementowy, to dowolny zbiór 4-elementowy, określamy jako: . Itd.- następnie zbiór 5-elementowy, itd.
Następne twierdzenie mówi o podstawowych własnościach sumy dwóch zbiorów:
Twierdzenie. 4.2. Dla dowolnych zbiorów , mamy:
Bardzo prosty dowód tego twierdzenia pozostawimy czytelnikowi. Dowód korzysta z określenia równości zbiorów / inkluzji, definicji sumy dwóch zbiorów, oraz z prostych praw rachunku zdań.
Przyjmiemy aksjomat ogólniejszy, dotyczący sumy dowolnej rodziny zbiorów.
Aksjomat sumy:
Zakładamy, że poniższa wypowiedź, zwana aksjomatem sumy, jest prawdą:
Dla dowolnej rodziny zbiorów , istnieje zbiór , tzn. zbiór, którego elementami są dokładnie wszystkie elementy wszystkich elementów .
Jeśli mamy zbiór zbiorów , ( rodzinę zbiorów), to - suma tej rodziny zbiorów, to nowy zbiór, którego elementami są dokładnie elementy elementów .
Jeśli . to , to zbiór złożony z wszystkich elementów , oraz wszystkich elementów , oraz wszystkich elementów , oraz wszystkich elementów - i tyle jego elementów. Sumowanie zbiorów należących do . Mówiąc prosto, mając zbiór zbiorów, tworzymy nowy zbiór, złożony z wszystkich elementów, tych że zbiorów.
Więc aksjomat ten mówi, że jeśli mamy rodzinę zbiorów, to możemy utworzyć sumę tej rodziny zbiorów. Aksjomat równości zbiorów, zapewnia jednoznaczność tej operacji- dla dowolnej, ustalonej rodziny zbiorów istnieje dokładnie jeden zbiór .- wniosek 5.1. Aby to udowodnić, weźmy dwa zbiory , , złożone dokładnie z elementów elementów , i pokażmy, że są równe. Wtedy:
przy pewnym zbiorze .
przy pewnym zbiorze .
Zauważmy, że prawe strony tych równoważności są do siebie równoważne. Jeśli jest elementem pewnego zbioru , z rodziny , to jest elementem pewnego zbioru , z rodziny - tzn., wystarczy przyjąć za zbiór , i wtedy . Analogicznie można uzasadnić, że jeśli jest elementem pewnego zbioru , z rodziny , to jest elementem pewnego zbioru , z rodziny . A więc prawe strony tych równoważności są do siebie równoważne, a więc również lewe strony są równoważne, czyli , co daje , co należało pokazać.
Podajmy podstawowe fakty odnośnie sum. Pierwszy z nich mówi, że suma pustej rodziny zbiorów jest dalej zbiorem pustym.
Fakt 5.2.: .
Dowód: GDYBY , to istniałoby , a więc zgodnie z określeniem sumy rodziny zbiorów , dla pewnego zbioru . Widzimy więc, że wtedy , a zbiór pusty nie posiada elementów-sprzeczność.
Kolejny fakt, jest nieco bardziej złożony:
Fakt 5.3.: .
Dowód: GDYBY , to istniałoby , a więc zgodnie z określeniem sumy rodziny zbiorów, , dla pewnego zbioru . Ponieważ, jedynym zbiorem w rodzinie , jest , to , i , sprzeczność.
Kolejny fakt jest uogólnieniem poprzedniego:
Fakt 5.4. Dla dowolnego zbioru , mamy: .
Dowód: Ustalmy dowolny zbiór , oraz dowolne . Wtedy , wtedy i tylko wtedy, gdy jest elementem elementu . Ponieważ, jedynym elementem , jest , to ostatnie zdanie jest równoważne temu, że . Wobec dowolności , otrzymujemy, że , co należało pokazać.
Następny fakt łączy sumę dwóch zbiorów z sumą rodziny zbiorów:
Fakt 5.5. Dla dowolnych zbiorów , mamy:
Dowód: W myśl twierdzenia 1.1., należy pokazać dwie inkluzje: , i
Aby pokazać pierwszą inkluzję, to niech . Oznacza to, że jest elementem elementu . Ale rodzina ma dwa elementy- zbiory . Wnioskujemy, że lub , czyli , i .
Aby pokazać drugą inkluzję, to niech . Oznacza to, że lub . Jeśli , to wtedy, ponieważ oczywiście , to jest elementem elementu , i . W przeciwnym przypadku, jeśli , to podobnie czytelnik łatwo wykaże, że również , w związku z czym Na mocy twierdzenia 1.1, otrzymujemy:
Kolejny dwa fakty są trochę bardziej nietypowe.
Fakt 5.6. Dla dowolnych rodzin zbiorów , mamy:
Już objaśniam- żeby to dobrze zrozumieć. Mamy dwie rodziny zbiorów , czyli - zbiór złożony ze zbiorów, oraz - drugi zbiór złożony ze zbiorów. Tworzymy najpierw zbiór (złożony ze zbiorów), i wtedy suma uogólniona takiej rodziny ma być równa sumie dwóch zbiorów- zbioru (zbioru będącego sumą uogólnioną pierwszej rodziny zbiorów) oraz zbioru (zbioru będącego sumą drugiej rodziny zbiorów).
Dowód:
Weźmy dwie rodziny zbiorów . Należy pokazać, że a więc inkluzje w prawo i w lewo.
Inkluzja w prawo:
Niech . Oznacza to, że , dla pewnego zbioru z rodziny . Wtedy , gdzie . Jeśli to jest elementem zbioru , z rodziny , a więc , a więc tymbardziej W pozostałym przypadku i wtedy podobnie , a więc również Wobec dowolności , inkluzja jest dowiedziona.
Inkluzja w lewo:
Niech . Oznacza to, że Jeśli , to jest elementem pewnego zbioru z rodziny . Wtedy zbiór , a więc , a więc element należy do zbioru z rodziny , zatem . Analogicznie można pokazać, że w pozostałym przypadku () również . Wobec dowolności , inkluzja jest dowiedziona, i
Następny fakt mówi,że jeśli jedna rodzina zbiorów zawiera się w drugiej rodzinie zbiorów, to również ich sumy pozostają w takiej zależności. Tzn.
Fakt 5.7. Dla dowolnych rodzin zbiorów , mamy:
Czyli mając rodzinę zbiorów dodając zbiory do tej rodziny, tworząc rodzinę zbiorów jeśli popatrzymy na sumy tych rodzin, to albo taka suma nie ulegnie zmianie, albo się istotnie zwiększy (pod względem inkluzji).
Dowód:
Weźmy dwie rodziny zbiorów , takie, że . Pokażemy, że . Niech . Oznacza to, że dla pewnego zbioru . Wiemy, że , wobec czego zbiór . Ponieważ jest elementem zbioru , z rodziny , to , co wobec dowolności elementu oznacza, że
Podamy teraz dwa ważne podstawowe twierdzenia odnośnie sumy rodziny zbiorów. Pierwsze twierdzenie mówi, że każdy zbiór z rodziny zbiorów jest podzbiorem sumy tej rodziny. Jest to podstawowa, bardzo ważna własność.
Twierdzenie 5.8. Jeśli jest rodziną zbiorów, a dowolnym zbiorem tej rodziny, to wtedy
Dowód: Aby pokazać, że to niech . Ponieważ zbiór , to jest elementem zbioru z rodziny , zatem , a więc
Ostatnia własność sumy, jaką podamy, jest też bardzo użyteczna. Wiemy, że suma rodziny zbiorów jest nadzbiorem każdego zbioru tej rodziny. Teraz pokażemy, że jest najmniejszym zbiorem o tej własności, tzn. jeśli zbiór jest nadzbiorem każdego zbioru rodziny, to jest nadzbiorem sumy rodziny. Najprościej mówiąc, stosuje się to jako: suma rodziny podzbiorów , jest również podzbiorem .
Twierdzenie 5.9. Jeśli jest rodziną zbiorów, a jest dowolnym zbiorem, i ponadto, dla każdego zbioru zachodzi , to wtedy
Czyli jeśli mamy rodzinę zbiorów, i każdy zbiór tej rodziny jest podzbiorem ustalonego zbioru , to wtedy suma tej rodziny jest również podzbiorem .
Dowód:
Powtórzmy założenia i oznaczenia dla tego twierdzenia. Pokażemy, że Niech . Oznacza to, że jest elementem zbioru - pewnego zbioru z rodziny . Ale wiemy też, że każdy zbiór z rodziny jest podzbiorem , więc w szczególności zbiór Ponieważ , to , i w efekcie
Aksjomat wybierania
Następny aksjomat mówi, że ze zbioru można wybrać podzbiór elementów spełniających konkretną własność.
Nim go wprowadzimy, należy wprowadzić tzw. formuły teoriomnogościowe. To nie są zbiory, to są wyrażenia logiczne podobne do tych, które już używaliśmy, tworzące język teorii mnogości. Zbudowane są one z formuł atomowych typu , , oraz formuł z nich powstałych poprzez stosowanie w skończenie wielu krokach operacji rachunku zdań , a także kwantyfikatorów . W praktyce jednak patrzymy na nie podobnie jak na formy zdaniowe- w tych wyrażeniach za zmienne wolne podstawiamy odpowiedniego rodzaju elementy, i otrzymujemy prawdę bądź fałsz. Zapis będzie oznaczał, że formuła ma dokładnie zmienne jako zmienne wolne.
Zakładamy, że poniższa wypowiedź, zwana aksjomatem wybierania (bądź wycinania), jest prawdą:
Dla dowolnej formuły , oraz dla dowolnego zbioru , istnieje zbiór złożony z dokładnie tych elementów , dla których prawdziwa jest formuła
Czyli dla zbioru , możemy utworzyć podzbiór złożony z tych elementów , dla których prawdą jest
Dla dowolnej formuły , oraz dla dowolnego zbioru , istnieje jedyny zbiór złożony z tych elementów , dla których prawdą jest -wniosek 6.1.
Aby to udowodnić, weźmy dwa zbiory złożone dokładnie z tych elementów dla których prawdą jest , i pokażmy, że , że są równe. Ustalmy dowolne . Wtedy oraz . Zatem , co daje , co należało pokazać.
Zbiór ten więc oznaczamy jako
Przyjmiemy aksjomat ogólniejszy:
Dla dowolnej formuły , dla dowolnych oraz dla dowolnego zbioru , istnieje zbiór złożony z dokładnie tych elementów , dla których prawdziwa jest formuła
To bardzo podobne co wcześniej. Różnica polega na tym, że mamy jeszcze jeden, lub dwa, lub ... skończenie wiele ustalonych elementów (od których zależy postać formuły ), i podobnie dla zbioru , możemy utworzyć podzbiór złożony z tych elementów , dla których prawdziwa jest formuła .
Podobnie, zbiór ten oznaczamy jako Te trudy pozwolą nam zdefiniować podstawowe operacje na zbiorach. Najpierw:
Dla dowolnych zbiorów zdefiniujmy ich iloczyn:
Jest to zbiór tych elementów, które występują w obu zbiorach równocześnie. Następne twierdzenie podaje podstawowe własności iloczynu zbiorów.
Twierdzenie 6.2. Dla dowolnych zbiorów , mamy :
Udowodnijmy, dla przykładu punkt 6.
Ustalmy dowolne . Wtedy wtedy i tylko wtedy, gdy , co, używając praw de'Morgana, jest równoważne , co znaczy , czyli to oznacza , co należało otrzymać.
Dowód punktu 7 jest analogiczny, dowody punktów 1-5 są bardzo proste, więc pozostawimy je czytelnikowi.
Zdefiniujmy dla dwóch zbiorów , ich różnicę:
Dla dwóch zbiorów ich różnica, to zbiór tych elementów, które występują w pierwszym zbiorze i nie występują w drugim zbiorze. Następne twierdzenie podaje podstawowe własności różnicy zbiorów.
Twierdzenie 6.3 Dla dowolnych zbiorów , mamy:
Dowód:
1. Ustalmy dowolne . Wtedy oznacza równoważnie i . Ostatni składnik koniunkcji znaczy , a więc . Wracając do całości otrzymujemy, że , a więc , Ponieważ pierwszy składnik alternatywy jest zawsze fałszem, otrzymujemy , czyli , co należało otrzymać.
4. Załóżmy, że , i przypuśćmy niewprost, że Oznacza to, że istnieje element , który , albo istnieje element , który nie jest elementem zbioru . Zajmijmy się pierwszym przypadkiem. Wtedy , więc powinien element , a więc powinno być , a w tym przypadku tak nie jest- sprzeczność. W drugim przypadku analogicznie otrzymujemy sprzeczność, co kończy dowód.
Proste dowody punktów 2,3 pozostawimy czytelnikowi.
Poniższe proste twierdzenie łączy inkluzje na zbiorach z działaniami mnogościowymi. Twierdzenie jest proste, choć sam ogólny schemat dowodu wykorzystuje pewien trik.
Twierdzenie 6.4. Niech będą zbiorami. Wtedy poniższe warunki są równoważne:
Schemat dowodu:
Chcemy pokazać, że Niewątpliwie Aby pokazać inkluzję w drugą stronę, to niech . Z założenia wynika, że . Zatem , i
Aby pokazać, że to najpierw zauważamy, że Z założeń otrzymujemy, że a więc taki zbiór, jako suma dwóch podzbiorów , jest podzbiorem , a więc i
Aby pokazać, że , podstawiamy na mocy założenia za zbiór , i otrzymujemy , gdyż każdy element , jest elementem .
Aby pokazać, że , to niech Gdyby było , to wtedy byłoby , zatem zbiór byłby niepusty- sprzeczność z założeniem . Zatem musi być , i
Z powyższego twierdzenia, wynika nie tylko, że przy zawieraniu zachodzą wypisane równości zbiorów, ale te wszystkie cztery warunki są równoważne. Zatem na przykład, gdy zbiór nie zawiera się w zbiorze , to wtedy na podstawie (3) , czyli Dowolne dwa z tych czterech warunków są równoważne, czyli dla dowolnych dwóch warunków z pierwszego wynika drugi, i z drugiego wynika pierwszy.
Dla dowolnej rodziny zbiorów , zdefiniujmy zbiór:
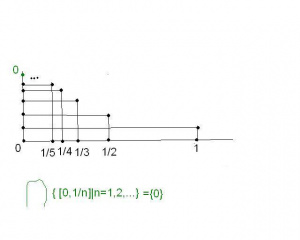
Czyli dla rodziny zbiorów , iloczynem (przekrojem) uogólnionym tej rodziny, jest to zbiór , złozony z tych elementów , które należą do każdego zbioru rodziny . Zobacz ilustrację obok przekroju trzech zbiorów.
Przykład: -zobacz obok rysunek.Z definicji iloczynu rodziny zbiorów wynika, że zawsze , a więc w szczególności , a więc Następne twierdzenie mówi, że jeśli tylko rodzina zbiorów jest niepusta, to definicje jej iloczynu można uprościć.
Twierdzenie 6.5. Jeśli , jest niepustą rodziną zbiorów, a dowolnym elementem, to zachodzi równoważność: należy do , wtedy i tylko wtedy, gdy należy do każdego zbioru rodziny .
To nie jest do końca tożsame z definicją , gdyż definicja ta mówi wpierw o wybieraniu elementów ze , tych elementów, które należą do każdego zbioru tej rodziny. A więc powyższe twierdzenie mówi, że jeśli tylko rodzina zbiorów jest niepusta, to warunek przynależności elementu do możemy opuścić( dla pustej rodziny zbiorów, dowolny element spełnia: choć ( formalnie) należy do każdego zbioru rodziny pustej- przypominam, zdanie postaci jest zawsze prawdziwe).
Dowód:
oczywisty, jeśli należy do , to z definicji znaczy to również, że, należy do każdego zbioru rodziny .
Załóżmy, że pokażemy, że Wystarczy zatem pokazać, że , i ponieważ z założenia należy do każdego zbioru rodziny , to również będzie należał do Ponieważ rodzina jest niepusta, więc istnieje zbiór Element należy do każdego zbioru rodziny , więc w szczególności . Ponieważ jest elementem zbioru , to , a więc
Podajmy proste fakty odnośnie iloczynu uogólnionego.
Fakt 6.6. Dla dowolnego zbioru , mamy:
Dowód: ustalmy dowolne . Ponieważ rodzina jest niepusta (bo jednoelementowa), więc jest równoważne temu (na mocy poprzedniego twierdzenia), że należy do każdego zbioru rodziny . Ponieważ jedynym zbiorem w rodzinie jest , więc to z kolei jest równoważne temu, że . Wobec dowolności -
Fakt 6.7. Dla dowolnych zbiorów , mamy:
Dowód: Należy pokazać inkluzje w obydwie strony: , oraz
Aby pokazać pierwszą inkluzję, to niech . Oznacza to, że i . Zatem dla dowolnego zbioru zachodzi , zatem ( rodzina jest niepusta ) , i
Aby pokazać drugą inkluzję, to niech . Wnioskujemy, że dla każdego zbioru . To z kolei oznacza, że i , a więc , i
Następny, podstawowy fakt mówi, że każdy zbiór z rodziny zbiorów jest nadzbiorem iloczynu tej rodziny zbiorów.
Twierdzenie 6.8. Jeśli jest rodziną zbiorów, a zbiorem tej rodziny, to
Dowód:
Niech Wnioskujemy, że jest elementem każdego zbioru rodziny . A więc w szczególności , i w efekcie
Wiemy, że iloczyn rodziny zbiorów jest podzbiorem każdego zbioru tej rodziny (w przeciwieństwie do sumy, która jest nadzbiorem każdego zbioru tej rodziny). Teraz pokażemy, że ten iloczyn jest największym zbiorem o tej własności. Najprościej mówiąc, stosuje się to jako: jeśli każdy zbiór z rodziny zbiorów jest nadzbiorem ustalonego zbioru , to wtedy iloczyn tej rodziny jest nadzbiorem .
Twierdzenie 6.9. Jeśli jest niepustą rodziną zbiorów, jest dowolnym ustalonym zbiorem, i dla każdego zbioru zachodzi , to wtedy
Czyli jeśli mamy niepustą rodzinę zbiorów, oraz zbiór , który jest podzbiorem każdego zbioru tej rodziny, to wtedy jest podzbiorem iloczynu tej rodziny zbiorów.
Dowód:
Powtórzmy założenia i oznaczenia dla tego twierdzenia. Pokażemy, że Niech Niech Ponieważ jest podzbiorem każdego zbioru z rodziny , więc również . Mamy zatem . Z dowolności zbioru , jest elementem każdego zbioru i ponieważ rodzina jest niepusta, to
Następny fakt mówi, że iloczyn większej rodziny zbiorów jest mniejszy, tzn. jeśli jedna rodzina zbiorów(niepusta) zawiera się w drugiej rodzinie zbiorów, to ich iloczyny spełniają inkluzję odwrotną.
Fakt 6.10. Jeśli jest niepustą rodziną zbiorów, a rodziną zbiorów, taką, że , to wtedy
Czyli mając niepustą rodzinę zbiorów dodając zbiory do tej rodziny, tworząc rodzinę zbiorów jeśli popatrzymy na iloczyny tych rodzin, to albo taki iloczyn nie ulegnie zmianie, albo się istotnie zmniejszy (pod względem inkluzji).
Dowód: Aby pokazać, że to niech . Wnioskujemy, że , dla każdego zbioru . Ponieważ , więc otrzymujemy, że , dla każdego zbioru . Zatem (rodzina jest niepusta) dostajemy
Aksjomat nieskończoności
Kolejny aksjomat mówi, że istnieje przynajmniej jeden zbiór do którego należą wszystkie liczby naturalne. Zbiór taki, musi więc być nieskończony.
Zakładamy, że poniższa wypowiedź, zwana aksjomatem nieskończoności, jest prawdą:
Istnieje rodzina zbiorów , taka że:
(1)
(2)
Rozważmy rodzinę zbiorów , o której mówi powyższy aksjomat. Z punktu (1) . Stosując (2) dla zbioru pustego, otrzymujemy, że . Stosując (2) dla otrzymujemy, że . Powtarzając to za każdym razem otrzymujemy nowy element zbioru Intuicyjnie, wymagania stawiane zbiorowi gwarantują, na zasadzie podobnej do indukcji matematycznej, że zbiór posiada nieskończenie wiele elementów. Zbiór ten może mieć jeszcze inne elementy, niż te, które udadzą się otrzymać w powyższy sposób.
Zbiór, którego istnienie gwarantuje aksjomat nieskończoności, jest używany do konstruowania zbioru liczb naturalnych. W konstrukcji von Neumanna zbioru liczb naturalnych, poniższe zbiory to kolejne liczby naturalne:
liczba naturalna zero to zbiór
liczba naturalna jeden to zbiór
liczba naturalna dwa to zbiór
liczba naturalna trzy to zbiór
i tak dalej ...
W powyższej konstrukcji liczba naturalna to bardzo konkretny zbiór( nie w całej matematyce, tylko w tej naszej konstrukcji, nie jest to oczywiście uniwersalna prawda matematyczna). Zbiór będący liczbą naturalną ma, intuicyjnie mówiąc, tyle elementów, jaka jest wartość tej liczby, choć nie każdy zbiór posiadający tyle elementów jest liczbą naturalną. Liczba naturalna , jest tutaj wzorcowym zbiorem -elementowym. W jednym z kolejnych rozdziałów zostanie dokładnie wprowadzony zbiór liczb naturalnych i związane z nim zagadnienia.
Aksjomat zbioru potęgowego
Aksjomat nieskończoności pozwala nam tworzyć zbiory nieskończone. Dzięki poniższemu aksjomatowi możemy tworzyć zbiory wszystkich podzbiorów danego zbioru. Jak będzie to przedstawione dalej, tworzenie zbioru złożonego z wszystkich podzbiorów danego zbioru, jest prostym sposobem na tworzenie jeszcze liczniejszych zbiorów. Wykażemy bowiem, że nawet dla zbiorów nieskończonych, zbiór wszystkich podzbiorów danego zbioru jest liczniejszy niż sam zbiór.
Zakładamy, że następująca wypowiedź, zwana aksjomatem zbioru potęgowego, jest prawdą:
Dla dowolnego zbioru istnieje zbiór , którego elementami są dokładnie wszystkie podzbiory .
A więc, aksjomat ten mówi, że jeśli mamy zbiór , to możemy utworzyć zbiór wszystkich jego podzbiorów. Nazywamy go zbiorem potęgowym zbioru , i oznaczamy przez . Dla dowolnego zbioru , mamy oczywiście: oraz zatem , oraz Proszę uważać, tak, należeć do zbioru potęgowego zbioru , znaczy zawierać się w . Proponuję więc, przestudiować uważnie poniższy prosty, lecz pouczający dowód.
Fakt 8.1. Dla dowolnych zbiorów mamy:
Czyli jeśli jeden zbiór zawiera się w drugim, to ich zbiory potęgowe pozostają w takiej(zgodnej) inkluzji.
Dowód:
Weźmy dwa zbiory , takie, że Pokażemy, że Niech zbiór Oznacza to, że Z założenia mamy więc z przechodniośći inkluzji zatem Z dowolności wyboru zbioru , otrzymujemy że
Kolejne ćwiczenie:
Ćwiczenie 8.2. Czy dla dowolnych zbiorów zachodzi równość:
Rozwiązanie: Udowodnijmy najpierw lemat, że dla dowolnego zbioru zachodzi:
Dla dowolnego zbioru , mamy a więc a więc z własności iloczynu więc Lemat jest więc udowodniony.
Aby dowieść twierdzenie, weźmy dowolne zbiory Na mocy udowodnionego przed chwilą lematu : ( jest również zbiorem, więc możemy do niego zastosować ten lemat); a prawa strona badanej równości jest równa na podobnej zasadzie: Równość jest więc prawdą.
Zbiór potęgowy zbioru niektórzy oznaczają przez Jeśli bowiem jest skończonym, -elementowym zbiorem, to ma elementów- będzie o tym mówiło kolejne ćwiczenie. Stąd też nazwa - zbiór potęgowy. My jednak pozostaniemy przy oznaczeniu
Ćwiczenie 8.3.: Wykaż, że jeśli jest skończonym, -elementowym zbiorem, to ma dokładnie elementów. Czy jeśli jest zbiorem, będącym liczbą naturalną, to czy zbiór jest liczbą naturalną oznaczoną nieformalnie jako ? (tzn. liczbą naturalną o wartości a potem traktowaną jako zbiór)?
Rozwiązanie:
Część pierwsza- używamy naiwnej formy indukcji.
Jeśli zbiór jest zeroelementowy, to , i posiada dokładnie element.
Załóżmy, że twierdzenie jest prawdą dla zbiorów -elementowych. Weźmy dowolny zbiór -elementowy , i wyróżnijmy w nim dowolny element . Łatwo zauważyć, że zbiór można podzielić na dwie części: zbiory do których należy , i zbiory do których nie należy . Te części mają tyle samo elementów, a więc tyle ile jest podzbiorów zbioru - zbioru -elementowego, a więc (na mocy założenia indukcyjnego) elementów. Wnioskujemy, że ma elementów, co należało pokazać.
Część druga- dla liczby naturalnej mamy: Tymczasem
a więc te zbiory są różne, bo
Aksjomat wyboru
Kolejnym aksjomatem jest aksjomat wyboru. Jest to aksjomat, który wywołał dużą ilość kontrowersji. Wielu znakomitych matematyków początku XX wieku uważało, że nie należy go dopuścić do zestawu podstawowych aksjomatów. W chwili obecnej większość matematyków uważa, że aksjomat wyboru jest prawdziwy, nawet jeśli jego konsekwencje są bardzo nieintuicyjne.
Przypomnijmy najpierw: Zbiory nazywamy rozłącznymi, gdy nie mają wspólnych elementów, tzn. Np. zbiory oraz zbiór są rozłączne.
Aksjomat wyboru:
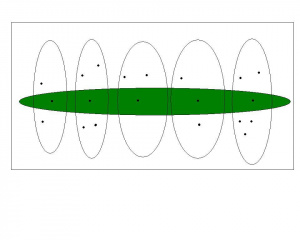
Dla dowolnej rodziny zbiorów niepustych ( tzn. jeśli ) i takiej, że każde dwa różne zbiory tej rodziny są rozłączne ( lub zbiory są rozłączne) to aksjomat wyboru głosi, że istnieje selektor tej rodziny zbiorów, tzn. taki zbiór , że:
dla dowolnego zbioru
tzn. selektor to zbiór , który ma po dokładnie jednym elemencie wspólnym z każdym zbiorem tej rodziny.
Intuicyjnie to znaczy, że mając niepustą rodzinę niepustych, rozłącznych zbiorów możemy utworzyć zbiór wybierając po jednym elemencie z każdego zbioru tej rodziny. Zbiór , gwarantowany przez aksjomat wyboru, wybiera z każdego zbioru tej rodziny dokładnie jeden element- zobacz ilustracja obok. Zbiory rodziny jako pionowe obszary, zbiór wybierający jako poziomy, zielony zbiór przecinający każdy zbiór rodziny na dokładnie jednym elemencie.
Wypada się zastanowić co się dzieje dla pustej rodziny zbiorów. Trochę nienaturalne jest stosowanie aksjomatu wyboru w takim wypadku, ale tego nie wykluczyliśmy (bo tak się na ogół robi), więc wypada sprawdzić czy na gruncie teorii mnogości bez aksjomatu wyboru zdanie, które jest aksjomatem wyboru zastosowanym do pustej rodziny jest prawdziwe. Aby to sprawdzić, zauważmy, że niestety pusta rodzina spełnia założenia aksjomatu wyboru- , i każde dwa zbiory w rodzinie pustej są (jakie chcemy- każde zdanie postaci jest prawdą) więc są równe lub rozłączne, wiec spełnione są założenia aksjomatu wyboru, więc połóżmy za dowolny zbiór, i wtedy dla dowolnego zbioru
Znowu, na tej zasadzie co wcześniej, dowolny zbiór w rodzinie pustej (będzie spełniał to co chcemy), czyli będzie miał ze zbiorem dokładnie jeden element wspólny. Czyli całe zdanie jest prawdą, i wszystko się zgadza ( przyjęliśmy je jako aksjomat, więc tak powinno być).