Aksjomat wyboru
Ten rozdział poświęcony jest konsekwencjom aksjomatu wyboru. Jest to aksjomat, który wywołał dużą ilość kontrowersji. Wielu znanych matematyków poddawało go w wątpliwość. W chwili obecnej znakomita większość uważa, że aksjomat wyboru jest prawdziwy, nawet jeśli niektóre z jego konsekwencji są nieintuicyjne.
W tym rozdziale przedstawiamy szereg twierdzeń, które są równoważne lub wynikają z aksjomatu wyboru. Zanim przejdziemy do wypowiedzi tych faktów, wprowadzimy jeszcze jeden termin.
Spis treści
Dobre uporządkowanie
Zbiór uporządkowany nazywamy zbiorem dobrze uporządkowanym, gdy każdy niepusty podzbiór ma element najmniejszy względem rozpatrywanego porządku . Mówimy wtedy, że zbiór jest dobrze uporządkowany przez , oraz, że jest dobrym porządkiem na zbiorze .
Przykładem zbioru dobrze uporządkowanego może być z naturalnym porządkiem. Zasada minimum mówi, że każdy niepusty podzbiór ma liczbę najmniejszą, a więc jest dobrze uporządkowany.
Fakt: Każdy zbiór dobrze uporządkowany jest również liniowo uporządkowany.
Dowód:
Niech będzie zbiorem dobrze uporządkowanym. Pokażemy, że jest również zbiorem liniowo uporządkowanym przez . Jeśli jest pusty lub jednoelementowy, to jest liniowo uporządkowany, W przeciwnym wypadku istnieją co najmniej dwa elementy . Weźmy więc dowolne dwa różne elementy - i . Rozważmy . Jest to dwuelementowy podzbiór . A ponieważ jest dobrze uporządkowany, to istnieje element najmniejszy . Jeśli , to . W przeciwnym przypadku , i wtedy . A więc elementy i są porównywalne. Z dowolności wyboru takich elementów, otrzymujemy, że jest liniowo uporządkowany przez .
Aksjomat wyboru
Zaczniemy od przytoczenia aksjomatu wyboru:
Dla dowolnej rodziny zbiorów niepustych i rozłącznych to aksjomat wyboru głosi, że istnieje selektor tej rodziny zbiorów, tzn. taki zbiór , że:
dla dowolnego zbioru
tzn. selektor to zbiór , który ma po dokładnie jednym elemencie wspólnym z każdym zbiorem tej rodziny.
Intuicyjnie to znaczy, że mając rodzinę rozłącznych zbiorów możemy utworzyć zbiór wybierając po jednym elemencie z każdego zbioru.
Będziemy zmierzać do dowodu twierdzenia Zermelo, że każdy zbiór da się dobrze uporządkować. Poza tym dowodem będziemy prezentować (na razie) tylko krótkie, proste dowody.
Twierdzenia dotyczące zbiorów
Pierwsze równoważne aksjomatowi wyboru twierdzenie mówi o funkcji wybierającej elementy ze zbiorów.
Dla dowolnej rodziny zbiorów zbiorów niepustych istnieje funkcja wyboru, tzn. funkcja , taka, że , dla każdego zbioru
Czyli mając rodzinę zbiorów niepustych możemy utworzyć funkcję, która tak: bierze zbiór niepusty i wybiera z niego jeden element, bierze następny zbiór niepusty i wybiera z niego jeden element, itd. dla dowolnego zbioru tej rodziny.
Zwróćmy uwagę, że co prawda funkcja ma spełniać , czyli przypisana wartość zbiorowi ma być elementem tego zbioru, ale ciężko powiedzieć którym, nie jest to jawnie powiedziane niestety. Ale korzystając z aksjomatu wyboru można wykazać, że taka funkcja istnieje (choć ciężko ją opisać wzorem jawnym).
Kolejne równoważne aksjomatowi wyboru twierdzenie to:
Dla dowolnych zbiorów , oraz dowolnej funkcji z 'na' zbiór , istnieje funkcja taka, że złożenie funkcji z funkcją jest równe - jest identycznością na zbiorze .
To twierdzenie jest równoważne aksjomatowi wyboru.
Aby to objaśnić, rozważmy funkcję , która jest 'na' zbiór ; i rozważmy rodzinę wszystkich przeciwobrazów zbiorów jednoelementowych z . Takie przeciwobrazy są zawsze niepuste. Aby się o tym przekonać to niech . Wtedy ponieważ jest 'na' , to przy pewnym . A zatem , czyli jest niepusty. Takie przeciwobrazy są również rozłączne. Utwórzmy przypisanie w poniższy sposób: , czyli elementowi przypisujemy element jego przeciwobrazu. Jeśli tak zrobimy, to w wyniku złożenia takiej funkcji z naszą funkcją , element powróci, czyli złożenie będzie mieć punkt stały, tzn. Jeśli elementowi przypisalibyśmy (znowu, przypisanie niech nazywa się ) element zbioru spoza , to złożenie nie będzie mieć punktu stałego dla , czyli , czyli nie będzie identycznością na . Jeśli dla każdego będziemy mu przypisywać element jego przeciwobrazu, to łatwo przypuścić, że złożenie będzie mieć w każdym punkcie punkt stały, stąd będzie identycznością na . Tyle tylko, że aby możliwe było utworzenie funkcji musimy wybrać dokładnie jeden element z wielu (na ogół) elementów jego przeciwobrazu. I tak dla każdego (przypominam to dowolne zbiory, to dowolna funkcja 'na')- dlatego to jest równoważne aksjomatowi wyboru- zobacz ilustrację obok. Dowód podamy później.
Twierdzenia dotyczące porządków
Kolejne równoważne aksjomatowi wyboru twierdzenie to twierdzenie o maksymalnym łańcuchu:
W każdym zbiorze uporządkowanym istnieje maksymalny łańcuch pod względem inkluzji.
Czyli w zbiorze uporządkowanym zawsze możemy znaleźć maksymalny łańcuch. Niestety, to o wiele trudniejszy problem niż jego brzmienie, ze względu na bogactwo zbiorów uporządkowanych, ich złożoność i możliwą nieskończoność. Jednak takie zadziwiające twierdzenie jest prawdziwe przy założeniu aksjomatu wyboru ( jest mu równoważne).
Poniższe twierdzenie jest równoważne twierdzeniu o maksymalnym łańcuchu, (a więc również aksjomatowi wyboru):
W każdym zbiorze uporządkowanym każdy łańcuch jest podzbiorem pewnego większego łańcucha maksymalnego.
To twierdzenie mówi, że jeśli mamy zbiór uporządkowany oraz łańcuch , to możemy dobrać do tego łańcucha większy łańcuch pod względem inkluzji, maksymalny.
Dowód jednego wynikania jest bardzo prosty( tego w tył akurat):
Załóżmy przytoczone twierdzenie. Pokazujemy twierdzenie o maksymalnym łańcuchu. Weźmy dowolny zbiór uporządkowany. Pokażemy że istnieje w nim łańcuch maksymalny pod względem inkluzji. Najpierw znajdźmy jeden łańcuch- zawsze możemy znaleźć łańcuch pusty. A więc mamy jeden łańcuch, i ponieważ do tego łańcucha możemy dobrać większy łańcuch pod względem inkluzji maksymalny (na mocy zakładanego twierdzenia), no to mamy łańcuch maksymalny, co należało pokazać.
Dowód wynikania w drugą stronę jest znacznie trudniejszy, więc go podamy później.
Kolejne równoważne aksjomatowi wyboru twierdzenie, to słynny Lemat Zorna:
Jeśli w zbiorze uporządkowanym każdy łańcuch ma ograniczenie górne, to istnieje w element maksymalny.
Dzięki temu twierdzeniu możemy uzyskać element maksymalny zbioru uporządkowanego. Łatwo pokazać, że Lemat Zorna jest równoważny twierdzeniu o maksymalnym łańcuchu.
Aby pokazać lemat Zorna, weźmy dowolny zbiór uporządkowany taki, że każdy łańcuch jest ograniczony od góry. Pokażemy, że istnieje w element maksymalny. Na mocy twierdzenia o maksymalnym łańcuchu znajdujemy maksymalny łańcuch pod względem inkluzji, nazwijmy go . Łańcuch ten ( jak każdy) posiada ograniczenie górne (nazwijmy je ), które jest porównywalne z każdym elementem , więc ponieważ jest maksymalnym łańcuchem to musi , a więc jest elementem i jest większe (słabo) od każdego elementu , zatem jest elementem największym , i ten element największy w , jest równocześnie elementem maksymalnym w całym . Gdyby tak nie było, to istniałby element . Ponieważ element jest większy od największego elementu , to . Zatem jest łańcuchem (co łatwo sprawdzić) istotnie większym od pod względem inkluzji, co przeczy maksymalności . Uzyskana sprzeczność kończy dowód.
Jako przykład zastosowania Lematu Zorna udowodnimy twierdzenie o maksymalnym antyłańcuchu:
W każdym zbiorze uporządkowanym istnieje maksymalny antyłańcuch pod względem inkluzji.
Czyli w zbiorze uporządkowanym możemy również zawsze znaleźć maksymalny antyłańcuch.
Dowód:
Ustalmy dowolny zbiór uporządkowany Rozważmy rodzinę wszystkich antyłańcuchów:
i uporządkujmy ją inkluzją. Wykażemy, że każdy łańcuch w ma ograniczenie górne.
Ustalmy w tym celu dowolny łańcuch Jako ograniczenie górne kładziemy , wpierw jednak musimy zapewnić, że ( ograniczenie górne musi być elementem zbioru uporządkowanego). Suma rodziny - rodziny antyłańcuchów, podzbiorów będzie podzbiorem . Aby wykazać, że jest antyłańcuchem, weźmy dowolne dwa różne elementy . Wtedy dla pewnego zbioru , oraz dla pewnego zbioru . Ponieważ jest łańcuchem pod względem inkluzji, to lub . Jeśli , to . Podobnie, w przeciwnym wypadku, jeśli to . Czyli są w lub są w . Ponieważ , zbiory są antyłańcuchami, więc ponieważ są różnymi elementami takiego antyłańcucha, wnioskujemy, że elementy są nieporównywalne. Pokazaliśmy, że dowolne dwa różne elementy są nieporównywalne, czyli jest antyłańcuchem, i należy do . Ponieważ jest nadzbiorem każdego zbioru rodziny , czyli jest większa pod względem inkluzji od każdego zbioru , stąd jest ograniczeniem górnym dla , tego łańcucha. Z dowolności wyboru zbioru każdy łańcuch w ma ograniczenie górne.
Stosując lemat Zorna wnioskujemy, że w zbiorze jest element maksymalny. Jest to poszukiwany maksymalny antyłańcuch pod względem inkluzji.
W sposób analogiczny (a nawet prostszy) można udowodnić przy pomocy Lematu Zorna dowieść twierdzenie o maksymalnym łańcuchu.
Twierdzenie Zermelo
Kolejne równoważne aksjomatowi wyboru twierdzenie to twierdzenie Zermelo. Mówi ono, że każdy zbiór da się dobrze uporządkować.
Twierdzenie Zermelo:
Dla każdego zbioru ( jeśli mamy dowolny zbiór, to można go dobrze uporządkować), a więc istnieje relacja w zbiorze , która jest dobrym porządkiem na tym zbiorze.
Kolejny dowód to: Lemat Zorna Twierdzenie Zermelo.
DOWÓD:
Ustalmy dowolny niepusty zbiór . (Dla zbioru pustego relacja pusta jest dobrym porządkiem na zbiorze pustym. Zbiór pusty jest liniowo uporządkowany, i zbiór pusty jest dobrze uporządkowany przez ten porządek pusty, gdyż każdy niepusty podzbiór zbioru pustego (a nie ma takich), więc każdy niepusty podzbiór zbioru pustego- będzie spełniał to co chcemy- czyli ma element najmniejszy, a więc jest to dobry porządek na zbiorze pustym, czyli zbiór pusty da się dobrze uporządkować). Dalej więc będzie dowolnym niepustym zbiorem.
Rozważmy rodzinę:
Będziemy mówić, że jest to rodzina wszystkich podzbiorów zbioru dobrze uporządkowanych wraz z dobrymi porządkami. Tam są wszystkie podzbiory zbioru dobrze uporządkowane, każdy element jest podzbiorem dobrze uporządkowanym (wraz z dobrym porządkiem), ale nie wiemy, które konkretnie podzbiory załapują się jako elementy tej rodziny, czyli czy są dobrze uporządkowane. Nie wiemy na przykład czy istnieje chociaż jeden dobry porządek na całym zbiorze . Tego nie wiemy, i na razie się nie dowiemy, gdyż to chcemy właśnie pokazać (dopiero się dowiemy gdy zakończymy ten dowód). Określmy przepiękną relację na elementach jako:
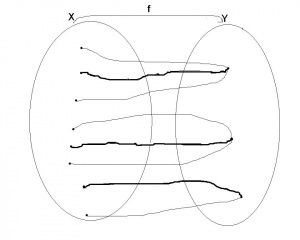
Czyli jeden zbiór dobrze uporządkowany jest mniejszy od drugiego zbioru dobrze uporządkowanego dokładnie wtedy, gdy pierwszy zbiór na którym jest określony pierwszy dobry porządek jest mniejszy pod względem inkluzji od drugiego zbioru na którym jest określony drugi dobry porządek, i porządek na większym zbiorze jest rozszerzeniem porządku na mniejszym zbiorze, przez dodanie elementów większych od wszystkich zastanych. Mówiąc prościej dobry porządek jest większy od danego dobrego porządku, gdy jest jego rozszerzeniem, ale dodając wyłącznie elementy większe od danych. To tak naprawdę bardzo naturalne, co ilustruje rysunek obok.
Wykazujemy najpierw, że jest to relacja porządku na
1.Zwrotność, czyli czy . A więc niewątpliwie , dla dowolnych mamy oczywiście, i jeśli więc warunek będzie pusto spełniony, a więc (jako całość) będzie spełniony, a więc mamy, że.
2.Antysymetria. Niech i . Z tego wynika, że oraz , a więc . Pokażemy że , to jednak łatwo wynika z warunku i faktu, że te relacje są określone na tym samym zbiorze. A więc , i co za tym idzie , co kończy dowód antysymetrii.
3. Przechodniość. Niech i . Pokażemy że . Pierwsze założenie daje , drugie podobnie , a więc z przechodniości inkluzji , co jest pierwszym z trzech warunków na to, by . Mamy dla dowolnych w mamy , a także dla dowolnych w mamy . Ponieważ , więc dla dowolnych w mamy . Możemy zatem to połączyć (pierwszy i trzeci z tych wniosków), i otrzymać, że dla dowolnych w mamy , co jest drugim sprawdzanym warunkiem. Niech . Pokażemy, że . Ponieważ , to , i jeśli, , to , co chciałem wykazać. Pozostaje zatem do rozważenia przypadek gdy: i (założenia), czyli , mamy więc , więc wnioskujemy, że , i ponieważ rozszerza , a więc , co było trzecim ostatnim warunkiem. A więc .
A więc jest zbiorem uporządkowanym. Aby móc zastosować do takiego zbioru uporządkowanego Lemat Zorna musimy wykazać, że każdy łańcuch w ma ograniczenie górne.
Niech będzie łańcuchem w sensie . Zdefiniujmy:
oraz
Tzn. zbiór to suma wszystkich zbiorów dobrze uporządkowanych z łańcucha , a jest sumą tych dobrych porządków określonych na tych zbiorach. Nim sprawdzimy, że jest ograniczeniem górnym tego łańcucha musimy zapewnić niestety, że Niewątpliwie . jako suma rodziny podzbiorów . Ponieważ elementy są zbiorami dobrze uporządkowanymi (a więc i liniowo) , ponieważ jest łańcuchem w sensie , więc tzn. między innymi, że dla dowolnych takich dwóch liniowych porządków jeden jest rozszerzeniem drugiego, więc w myśl twierdzenia z rozdziału Zbiory Uporządkowane ( pod koniec) jest liniowym porządkiem na swoim polu. Łatwo się przekonać, że tym polem jest dokładnie zbiór . Aby wykazać, że jest dobrym porządkiem na , weźmy dowolny niepusty zbiór Ponieważ jest niepustym podzbiorem sumy zbiorów, więc istnieje zbiór , taki, że , że ten zbiór ten zbiór przecina. Ponieważ , to jest zbiorem dobrze uporządkowanym, w związku z czym zbiór ma element najmniejszy w , oznaczmy go przez . Element najmniejszy w jest elementem tego zbioru, a więc jest również elementem . Element będzie również elementem najmniejszym w Aby to wykazać, niech Jeśli , to , a ponieważ jest elementem najmniejszym w względem , to , a więc tymbardziej (), a więc , A więc jest mniejszy od . Jeśli , ponieważ przecież , więc dla pewnego , wtedy również Ponieważ jest łańcuchem elementy oraz , są porównywalne, przypadek zajść nie może, bo on prowadzi do , co stoi w sprzeczności z tym, że , wobec czego musi zajść relacja w drugą stronę, czyli , więc stosując trzecią część definicji do oraz wnioskujemy, że a więc tym bardziej , a więc również jest mniejszy od . Wnioskujemy, że jest najmniejszym elementem , względem . Z dowolności wyboru zbioru , każdy niepusty podzbiór ma element najmniejszy, względem . A więc jest zbiorem dobrze uporządkowanym, mamy też , zatem mamy podzbiór zbioru dobrze uporządkowany, a więc element zbioru . Należy teraz sprawdzić, że taki element jest ograniczeniem górnym tego łańcucha. W tym celu niech Należy pokazać, że . Z własności sumy spełniony jest punkt pierwszy w definicji , tzn. Jak również spełniony jest punkt drugi na podobnej zasadzie. Aby sprawdzić punkt trzeci to niech Wtedy , więc w sposób analogiczny jak wcześniej sprawdzamy, że . A więc spełniony jest również punkt trzeci, więc , i z dowolności wyboru elementu otrzymujemy, że jest ograniczeniem górnym dla - tego łańcucha, i z dowolności wyboru łańcucha każdy łańcuch w ma ograniczenie górne.
Stosując Lemat Zorna wnioskujemy, że w zbiorze uporządkowanym jest element maksymalny. Taki element maksymalny jest elementem zbioru uporządkowanego , czyli w tym wypadku podzbiorem zbioru dobrze uporządkowanym, oznaczmy go . Jeśli zatem , to ten dobry porządek na zbiorze równym świadczy o tym, że zbiór da się dobrze uporządkować. Pozostaje przyjąć dla dowodu nie wprost, że tak nie jest. Przypominam, element maksymalny jest podzbiorem zbioru dobrze uporządkowanym. Przypuszczamy dla dowodu nie wprost, że jest on określony na istotnym podzbiorze . Istnieje wtedy element . Ustalmy taki element . A wtedy zbiór wraz z dobrym porządkiem określonym jako :
Jest to zbiór z dodanym jednym elementem jako największym. Jest to dobry porządek, gdyż był dobrym porządkiem na , zatem jest również zbiorem dobrze uporządkowanym, podzbiorem zbioru dobrze uporządkowanym, zatem jest elementem . I jest elementem silnie większym w sensie od elementu maksymalnego . Jest od niego różny, bo jest określony na innym zbiorze, na większym zbiorze o jeden element , zatem są to różne zbiory dobrze uporządkowane, i jest większy od w sensie , gdyż jest jego rozszerzeniem przez dodanie jednego elementu większego od wszystkich zastanych, więc jest większy względem . A ponieważ był elementem maksymalnym, to nie ma w elementów od niego silnie większych. Otrzymaliśmy więc sprzeczność, która kończy rozumowanie.
Znaczenie tego twierdzenia podamy później.