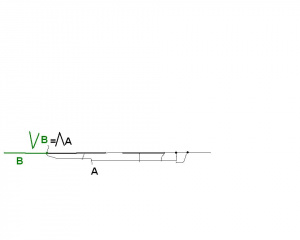Dalsze zagadnienia: Różnice pomiędzy wersjami
| Linia 184: | Linia 184: | ||
Niech <math>\left( X, \le \right)</math> będzie zbiorem uporządkowanym, w którym każdy niepusty podzbiór ograniczony z góry ma supremum. Pokażemy, że również każdy niepusty podzbiór ograniczony z dołu ma infimum. Niech <math>A \subset X</math> będzie niepustym podzbiorem ograniczonym z dołu. Chcemy pokazać, że ma infimum. Rozważmy zbiór <math>B</math> wszystkich ograniczeń dolnych <math>A</math> (czyli zbiór na lewo od <math>A</math>). Ponieważ <math>A</math> jest ograniczony z dołu, więc ma ograniczenie dolne, stąd zbiór <math>B</math> jest niepusty. Zbiór <math>B</math> jest podzbiorem <math>X</math> ograniczonym z góry przez elementy <math>A \neq \left\{ \right\}.</math> Zatem, z założenia, <math>B</math> ma supremum, i pokazujemy, że to supremum jest infimum zbioru <math>A</math> (na prawo).<math>\square</math> (Ilustracja taka sama jak przedtem). | Niech <math>\left( X, \le \right)</math> będzie zbiorem uporządkowanym, w którym każdy niepusty podzbiór ograniczony z góry ma supremum. Pokażemy, że również każdy niepusty podzbiór ograniczony z dołu ma infimum. Niech <math>A \subset X</math> będzie niepustym podzbiorem ograniczonym z dołu. Chcemy pokazać, że ma infimum. Rozważmy zbiór <math>B</math> wszystkich ograniczeń dolnych <math>A</math> (czyli zbiór na lewo od <math>A</math>). Ponieważ <math>A</math> jest ograniczony z dołu, więc ma ograniczenie dolne, stąd zbiór <math>B</math> jest niepusty. Zbiór <math>B</math> jest podzbiorem <math>X</math> ograniczonym z góry przez elementy <math>A \neq \left\{ \right\}.</math> Zatem, z założenia, <math>B</math> ma supremum, i pokazujemy, że to supremum jest infimum zbioru <math>A</math> (na prawo).<math>\square</math> (Ilustracja taka sama jak przedtem). | ||
| + | |||
| + | |||
| + | |||
| + | [[Plik:Suma_liniowych_porządów-_supremum.JPG|300px|thumb|right|]] | ||
| + | Niech <math>X</math> będzie zbiorem. Rozważmy rodzinę <math>\mathbb{B}</math> wszystkich liniowych porządków na jakichkolwiek podzbiorach zbioru <math>X</math>, wraz z inkluzją. Ponieważ są to liniowe porządki na pewnych zbiorach <math>Y \subset X</math>, więc w szczególności relacje w tych zbiorach <math>Y \subset X</math>, więc łatwo się przekonać, że te relacje są podzbiorami <math>X \times X</math> (więc są również relacjami w zbiorze <math>X</math>), więc są podzbiorami ustalonego zbioru, więc inkluzja na takiej rodzinie zbiorów jest relacją porządku, stąd <math>\left( \mathbb{B}, \subset\right)</math> jest zborem uporządkowanym. Liniowy porządek jest większy od danego gdy jest jego nadzbiorem, lub inaczej mówiąc gdy jest jego rozszerzeniem. Łatwo więc będzie pokazać, że również w <math>\left( \mathbb{B}, \subset\right)</math> każdy niepusty łańcuch posiada supremum. | ||
| + | |||
| + | Niech <math>\mathbb{D} \subset \mathbb{B}</math> będzie niepustym łańcuchem. Wtedy jeśli mamy dwa elementy <math>\mathbb{D}</math>, to są one liniowymi porządkami, i są porównywalne względem <math>\subset</math> , a wiec jeden z nich jest rozszerzeniem drugiego, więc w myśl twierdzenia o sumie liniowych porządków( Zbiory uporządkowane pod koniec) relacja <math>\bigcup \mathbb{D}</math> jest liniowym porządkiem na swoim polu, czyli na podzbiorze zbioru <math>X</math>. Zatem <math>\bigcup \mathbb{D} \in \mathbb{B}</math> Z własności sumy <math>\bigcup \mathbb{D}</math> jest supremum względem inkluzji dla <math>\mathbb{D}.\square</math> Zobacz ilustrację obok. | ||
| + | |||
| + | |||
| + | [[Plik:Rozkłady_zbioru.JPG|300px|thumb|rigt|]] | ||
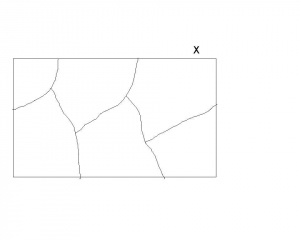
| + | Niech <math>X</math> będzie niepustym zbiorem. Rodzinę <math>\mathbb{B}</math> podzbiorów <math>X</math> nazywamy rozkładem | ||
| + | (podziałem) zbioru <math>X</math>, gdy: | ||
| + | |||
| + | <math>1. \ A \neq \left\{ \right\} ,</math> dla dowolnego <math>A \in \mathbb{B}. </math> | ||
| + | |||
| + | <math>2. \ \bigcup \mathbb{B}=X,</math> | ||
| + | |||
| + | <math>3. \ (A\in\mathbb{B}\wedge B\in\mathbb{B} \wedge A \neq B )\Longrightarrow A\cap B =\left\{ \right\}.</math> | ||
| + | |||
| + | |||
| + | Czyli jest to rodzina zbiorów niepustych, których suma wynosi <math>X</math>, i tak, że każde dwa różne zbiory tej rodziny są rozłączne, (czyli wtedy <math>A\cap B =\left\{ \right\}</math>- ich przekrój jest zbiorem pustym). Intuicyjnie jest to dowolne pokrojenie zbioru <math>X</math> na kawałki- zobacz ilustracje obok. | ||
| + | |||
| + | Dla dowolnego niepustego zbioru <math>X</math> przykładem jego rozkładu może być rodzina <math>\left\{ \left\{ x\right\}\Bigl| \ \ x\in X \right\}</math> wszystkich zbiorów jednoelementowych( co łatwo sprawdzić). Jest to "najdrobniejszy" rozkład zbioru <math>X</math>. Przy okazji zauważmy (prawdziwy) fakt, że dla dowolnego rozkładu <math>\mathbb{B}</math> zbioru <math>X</math> jego moc (ilość elementów <math>\mathbb{B}</math>) jest co najwyżej taka jak moc zbioru <math>X</math>. | ||
Wersja z 23:55, 28 lip 2019
Będę tu prezentował dodatkowe, raczej proste zadania( bo były fajne zadania, które zostawiłem na potem). Będą to raczej proste problemy.
Uzasadnimy najpierw, że dla dwóch rodzin zbiorów nie zawsze zachodzi równość zbiorów:
Jako kontrprzykład dla tej równości połóżmy oraz
Wtedy , podobnie , zatem
Podczas gdy , bo zbiory , zatem , równość więc nie jest prawdą.
Zastanówmy się nad inkluzjami dla rodziny zbiorów : , oraz Otóż, wbrew pozorom, ta ostatnia inkluzja jest o wiele bardziej nietypowa. Pierwsza inkluzja mówi, że elementy są elementami , czyli elementy elementów (zbiorów rodziny ) są elementami - są to tzw. zbiory(rodziny zbiorów) przechodnie. Równoważnie to możemy określić warunkiem , bo ten warunek oznacza, że zbiory rodziny są elementami , czyli są podzbiorami , w związku z czym ich elementy są elementami , czyli to oznacza, że elementy elementów są elementami . O takich zbiorach przechodnich będziemy jeszcze pisać.
Natomiast inkluzja jest o wiele dziwniejsza. Mówi ona, że zbiory rodziny są elementami , a więc elementów tych zbiorów. A to przecież elementy zbiorów rodziny są elementami odpowiednich zbiorów. Jednak taka dziwaczna inkluzja jest możliwa. Niech będzie dowolną rodziną induktywną (tzn. spełniającą aksjomat nieskończoności). Wykażemy, że wtedy
Niech Pokażemy, że Ponieważ jest zbiorem induktywnym, to , ponieważ , to
Zastanówmy się teraz uważnie nad pytaniem: Czy istnieje więcej niż jeden zbiór(rodzina zbiorów) taka, że ?
Otóż wiemy, że dla dowolnego zbioru mamy a więc istnieje przynajmniej jedna taka rodzina zbiorów. Biorąc teraz dwa różne zbiory , zauważamy, że wtedy rodziny zbiorów są różne (bo zbiory są różne). Zgodnie z przytoczonym faktem oraz , wobec czego istnieją co najmniej dwie rodziny zbiorów , takie,że iloczyn rodziny jest równy sumie rodziny .
Dla dowolnego zbioru , mamy:
Dowód: Aby pokazać, że pokazujemy dwa zawierania.
Inkluzja w prawo: Suma rodziny wszystkich podzbiorów , a więc suma szczególnej rodziny podzbiorów musi być podzbiorem .
Inkluzja w lewo: Wiemy,że suma dowolnej rodziny zbiorów jest nadzbiorem każdego zbioru tej rodziny, więc suma rodziny wszystkich podzbiorów jest nadzbiorem (bo , a więc ).
A więc
Dla dowolnej rodziny zbiorów mamy:
Dowód: Niech . Skoro jest zbiorem z rodziny , to z własności sumy jest podzbiorem sumy tej rodziny, czyli To z kolei oznacza, że , i z dowolności , otrzymujemy
Jednak inkluzja w drugą stronę nie zawsze zachodzi. Kontrprzykładem będzie rodzina Wtedy:
bo , bo Zatem tutaj
Jeśli mamy funkcję , to element nazywamy punktem stałym funkcji , gdy
Niech będzie zbiorem. Rozważmy funkcję określoną jako:
Czyli funkcja dostaje jako argument rodzinę podzbiorów , i przypisuje jej rodzinę złożoną z dwóch zbiorów- zbioru będącego sumą tej rodziny oraz zbioru będącego iloczynem tej rodziny. Podamy kilka przykładów punktów stałych dla tej funkcji.
Dla dowolnego zbioru , mamy A więc rodzina jest punktem stałym. Kolejne przykłady:
Dla dowolnego zbioru , mamy
Dla dowolnych zbiorów , takich, że mamy: gdzie przedostatnia równość pochodzi z założenia, że
Zwróćmy uwagę, że istnieją funkcje, które nie mają punktów stałych. Prostym przykładem może być funkcja daną jako
Kolejny przykład. Niech będzie niepustym zbiorem. Wykażemy, że dla funkcji określonej jako , nie istnieje punkt stały.
Przypuśćmy, że istnieje punkt stały, nazwijmy go . Wtedy Z drugiej strony, z definicji tej funkcji mamy Wnioskujemy, że Ponieważ zbiór jest niepusty, więc istnieje element ustalamy taki element. Rozstrzygnijmy problem czy Jeśli tak, to z tej równości wynika, że , a więc z definicji różnicy zbiorów - sprzeczność. Jeśli , to a więc z tej równości wynika, że , i również otrzymujemy sprzeczność, co kończy ten prosty dowód.
Dla funkcji zbiór nazywamy najmniejszym punktem stałym, gdy (czyli jest punktem stałym) oraz dla dowolnego zbioru spełniony jest warunek Czyli gdy każdy punkt stały jest większy pod względem inkluzji od - od tego najmniejszego punktu stałego, czyli zbiór jest nadzbiorem zbioru .
Podobnie dla funkcji zbiór nazwiemy największym punktem stałym, gdy jest punktem stałym, oraz każdy zbiór będący punktem stałym jest podzbiorem , czyli wtedy zbiór jest większy pod względem inkluzji od .
Poniższy przykład pokazuje, że dla funkcji może się zdarzyć, że mimo, że istnieją punkty stałe, ale nie istnieje największy punkt stały.
Niech będzie niepustym zbiorem. Rozważmy funkcję , określoną jako czyli funkcja dostaje jako argument rodzinę podzbiorów , i przypisuje jej zbiór jednoelementowy złożony z sumy tej rodziny. Jeśli jest rodziną podzbiorów , która jest punktem stałym, to wtedy Widać więc, że punktami stałymi mogą być tylko rodziny jednozbiorowe (jednoelementowe)- bo zbiór jest jednoelementowy. Wykażemy teraz, że każda rodzina jednozbiorowa jest punktem stałym. Niech Pokazujemy, że jest punktem stałym. Z określenia funkcji mamy Zatem jest punktem stałym. Zatem dla tej funkcji punktami stałymi są dokładnie rodziny jednozbiorowe. Ponieważ jest niepusty, więc ma co najmniej dwa różne podzbiory (np. i ). Ustalmy dwa takie różne podzbiory Wtedy rodziny zbiorów są różne ( bo zbiory są różne). Zgodnie z udowodnioną własnością rodziny zbiorów są punktami stałymi. Gdyby istniał tu największy punkt stały, to musiałby być nadzbiorem oraz zatem musiałby mieć co najmniej dwa elementy (). A ponieważ jest to punkt stały, i punktami stałymi są dokładnie rodziny jednozbiorowe otrzymujemy sprzeczność. Wobec czego tu nie istnieje największy punkt stały ( choć istnieją co najmniej dwa punkty stałe).
Jednak każda funkcja , która jest monotoniczna ze względu na inkluzję, posiada najmniejszy punkt stały oraz ma największy punkt stały.
Monotoniczna pod względem inkluzji, tzn. spełnia warunek dla dowolnych zbiorów :
Warunek ten mówi, że jeśli na argumentach funkcji zachodzi inkluzja (przypominamy,że argumentami i wartościami funkcji są tu podzbiory zbioru ), to na odpowiadających im wartościach również zachodzi (zgodna) inkluzja. Funkcję monotoniczne ze względu na inkluzję zachowują relację inkluzji pomiędzy przekształcanymi zbiorami.
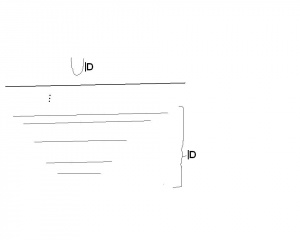
Przypomnijmy intuicję ze szkoły, że funkcja pomiędzy dwoma zbiorami, to przyporządkowanie każdemu elementowi pierwszego zbioru dokładnie jednego elementu drugiego zbioru. U nas rolę przyporządkowania w sposób ścisły pełni relacja pomiędzy tymi zbiorami. Każda funkcja jest zatem zbiorem par uporządkowanych. Spróbujemy jednak zilustrować funkcję za pomocą grafu. Wiemy, że funkcja jest zbiorem par, a każdy zbiór jest (sam w sobie) nieuporządkowany. Możemy zatem te pary ustawić w takiej kolejności jak chcemy. Weźmy element dziedziny , z definicji funkcji jest mu przypisany dokładnie jeden element . Łączymy te elementy, łączymy wszystkie elementy dziedziny którym jest przypisana wartość z elementem . Bierzemy kolejny inny element dziedziny funkcji , przypisany jest mu jeden element . Łączymy te elementy, łączymy wszystkie elementy dziedziny którym jest przypisana wartość z elementem . Bierzemy kolejny inny element dziedziny funkcji , robimy ten proces aż się wyczerpią elementy dziedziny(u nas cztery serie- zobacz ilustrację obok).
Jeśli funkcja jest bijekcją, to relacja odwrotna jest funkcją bijekcją ze zbioru w zbiór .
Dowód:
Pokażemy, że Niech Ponieważ jest bijekcją, to jest 'na' zbiór , więc przy pewnym . Inaczej mówiąc . Wtedy z określenia relacji odwrotnej , a więc należy do . Wobec dowolności wyboru otrzymujemy
Pokażemy, że relacja jest funkcją ze zbioru w zbiór . Przypuśćmy dla dowodu nie wprost, że nie jest funkcją. Oznacza to, że istnieje element oraz elementy takie, że , i Wtedy i inaczej mówiąc i ponieważ jest bijekcją, więc jest różnowartościowa, więc otrzymujemy sprzeczność wobec tego, że ta funkcja różnym elementom przypisuje tą samą wartość
Pokażemy, że funkcja jest funkcją różnowartościową. Weźmy dowolne pary należące do niej które mają taką samą drugą współrzędną . Pokażemy, że Ponieważ to i , wobec czego, i ponieważ jest funkcją, otrzymujemy . Zatem jest funkcją różnowartościową.
Pokażemy, że funkcja jest 'na' zbiór . Niech . Ponieważ , to istnieje jedyny element , taki, że Inaczej mówiąc , a więc , inaczej mówiąc , a więc jest wartością funkcji Wobec dowolności ,funkcja jest 'na' zbiór
Zatem jest funkcją bijekcją ze zbioru w zbiór
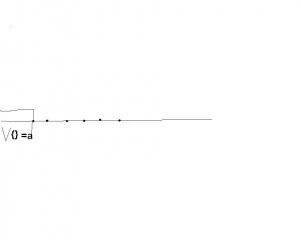
Wykażemy, że jeśli w zbiorze uporządkowanym jest element najmniejszy, to jest on supremum zbioru pustego, ( pustego podzbioru ). Zobacz ilustrację obok.
Niech będzie elementem najmniejszym w . Pokażemy, że spełnia warunki bycia supremum
1. Należy pokazać, że jest ograniczeniem górnym zbioru pustego, czyli dla dowolnego , oczywiście jest to (formalnie) prawda.
2. Niech będzie ograniczeniem górnym zbioru pustego. Ponieważ jest elementem najmniejszym, to natychmiast otrzymujemy, że . Wobec dowolności oznacza, to że
W sposób symetryczny można pokazać, że jeśli w zbiorze uporządkowanym jest element największy, to jest on infimum zbioru pustego, ( pustego podzbioru ).
W zbiorze uporządkowanym jeśli każdy podzbiór ma supremum, to każdy podzbiór ma infimum.
Przedstawmy jedynie piękny szkic dowodu.
Niech będzie zbiorem uporządkowanym w którym każdy podzbiór ma supremum. Należy pokazać, że każdy podzbiór ma infimum. Weźmy zbiór . Należy pokazać, że ma infimum. Rozważmy zbiór na lewo od zbioru ( czyli zbiór ograniczeń dolnych zbioru ). Taki zbiór jako podzbiór ma supremum, i pokazujemy, że to supremum jest infimum zbioru na prawo. Zobacz ilustrację obok.
W sposób symetryczny, w zbiorze uporządkowanym, jeśli każdy podzbiór ma infimum, to każdy podzbiór ma supremum.
Symetrycznie- trzeba wziąć zbiór , i rozważyć zbiór na prawo od niego. Taki zbiór ma infimum, i pokazujemy, że to infimum jest supremum zbioru na lewo- zbioru .
Niech będzie zbiorem. Wtedy rodzina jego wszystkich podzbiorów jest uporządkowana przez inkluzję, zatem jest zbiorem uporządkowanym. Wtedy mówiliśmy, że dla dowolnej rodziny , mamy a jeśli dodatkowo rodzina jest niepusta, to Objaśniając, jeśli weźmiemy rodzinę podzbiorów , wtedy supremum tej rodziny jest suma tej rodziny, a jeśli dodatkowo rodzina jest niepusta, to jej infimum to iloczyn tej rodziny. Dla pustej rodziny, mamy, jej infimum to element największy( mówiliśmy, że element największy jest infimum zbioru pustego), czyli tutaj cały zbiór ( jest największym elementem pod względem inkluzji), podczas gdy Równość więc dla niepustego zbioru nie ma miejsca.
Relacja w zbiorze jest zwrotna dokładnie wtedy, gdy zawiera relację identyczności na . Zilustrujmy to lepiej- zobacz obok.
Relacja jest symetryczna, jeśli spełnia warunek (dla dowolnych )
Czyli jeśli elementy są ze sobą w relacji , to symetrycznie są również w relacji .
Przykład: Niech Taka relacja jest symetryczna. Niech Natomiast relacja nie jest symetryczna, bo , podczas gdy
Relacja symetryczna jest symetryczna względem przekątnej- zobacz ilustrację obok.
Niech będzie zbiorem, a relacją w tym zbiorze. Wtedy poniższe warunki są równoważne.
(1) jest symetryczna,
(2)
Czyli jest symetryczna, równoważnie gdy jest równa swojej relacji odwrotnej.
Dowód:
Załóżmy, że jest symetryczna. Aby pokazać, że pokazujemy dwie inkluzję. Inkluzja w prawo: Niech Wtedy ponieważ jest symetryczna, więc a więc z określenia relacji odwrotnej Zatem Inkluzja w lewo: Niech Wtedy z określenia relacji odwrotnej Ponieważ jest symetryczna, więc również Zatem i
Załóżmy, że Aby pokazać, że jest symetryczna, to niech Wtedy z założonej równości a więc z określenia relacji odwrotnej Wnioskujemy, że jest symetryczna.
Jako przykład zastosowania tego twierdzenia, wykażemy, że suma dwóch relacji symetrycznych na tym samym zbiorze jest relacją symetryczną.
Niech będzie zbiorem, a relacjami symetrycznymi w zbiorze . Wykażemy, że relacja jest relacją symetryczną.
Dowód:
Ponieważ są relacjami symetrycznymi, więc , i Wobec czego:
czyli a więc relacja jest symetryczna.
Wykażemy, że w każdym niepustym skończonym podzbiorze liniowo uporządkowanego zbioru jest element najmniejszy i największy.
Niech będzie zbiorem liniowo uporządkowanym, a niepustym skończonym podzbiorem. Wykażemy, że w jest element najmniejszy i największy. Dowód poprowadzimy indukcyjnie ze względu na ilość elementów zbioru .
Jeśli jest jednoelementowy, tzn. , to wtedy ten element jest jego elementem najmniejszym i największym.
Przypuśćmy, że twierdzenie zachodzi dla zbiorów -elementowych (). Weźmy dowolny ()-elementowy zbiór . Ustalmy . Rozważmy jest to zbiór -elementowy, zatem możemy zastosować do niego założenie indukcyjne, i dostać jego element najmniejszy i największy . Wtedy ponieważ jesteśmy na zbiorze liniowo uporządkowanym, więc elementy i są porównywalne, i wtedy mniejszy z elementów i jest elementem najmniejszym ( bo jest najmniejszy w ). Podobnie, większy z elementów i jest elementem największym . Dowolność zbioru kończy dowód kroku indukcyjnego, i cały dowód.
Możemy podać oczywisty przykład zbioru uporządkowanego w którym każdy łańcuch posiada supremum.
Oczywistym przykładem jest dowolny skończony zbiór uporządkowany w którym jest element najmniejszy . Pokażemy, że w zbiorze każdy łańcuch posiada supremum. Ustalmy dowolny łańcuch . Jeśli , to ponieważ jest elementem najmniejszym w całym , więc jest to supremum pustego łańcucha. Jeśli łańcuch jest niepusty, to ponieważ jest podzbiorem zbioru -zbioru skończonego, więc jest skończony. A w skończonym zbiorze niepustym liniowo uporządkowanym (bo jest to łańcuch, więc jest on liniowo uporządkowany przez dany porządek ograniczony do elementów tego łańcucha) jest element największy. Ponieważ jest elementem największym łańcucha , to tym bardziej jest jego supremum.
W zbiorze uporządkowanym zbiór nazywamy ograniczonym z góry, jeśli ma on w ograniczenie górne.
Podobnie zbiór nazwiemy ograniczonym z dołu, jeśli ma on ograniczenie dolne.
Wykażemy, że jeśli w zbiorze uporządkowanym każdy niepusty podzbiór ograniczony z góry ma supremum, to każdy niepusty podzbiór ograniczony z dołu ma infimum.
Dowód( szkic):
Niech będzie zbiorem uporządkowanym, w którym każdy niepusty podzbiór ograniczony z góry ma supremum. Pokażemy, że również każdy niepusty podzbiór ograniczony z dołu ma infimum. Niech będzie niepustym podzbiorem ograniczonym z dołu. Chcemy pokazać, że ma infimum. Rozważmy zbiór wszystkich ograniczeń dolnych (czyli zbiór na lewo od ). Ponieważ jest ograniczony z dołu, więc ma ograniczenie dolne, stąd zbiór jest niepusty. Zbiór jest podzbiorem ograniczonym z góry przez elementy Zatem, z założenia, ma supremum, i pokazujemy, że to supremum jest infimum zbioru (na prawo). (Ilustracja taka sama jak przedtem).
Niech będzie zbiorem. Rozważmy rodzinę wszystkich liniowych porządków na jakichkolwiek podzbiorach zbioru , wraz z inkluzją. Ponieważ są to liniowe porządki na pewnych zbiorach , więc w szczególności relacje w tych zbiorach , więc łatwo się przekonać, że te relacje są podzbiorami (więc są również relacjami w zbiorze ), więc są podzbiorami ustalonego zbioru, więc inkluzja na takiej rodzinie zbiorów jest relacją porządku, stąd jest zborem uporządkowanym. Liniowy porządek jest większy od danego gdy jest jego nadzbiorem, lub inaczej mówiąc gdy jest jego rozszerzeniem. Łatwo więc będzie pokazać, że również w każdy niepusty łańcuch posiada supremum.
Niech będzie niepustym łańcuchem. Wtedy jeśli mamy dwa elementy , to są one liniowymi porządkami, i są porównywalne względem , a wiec jeden z nich jest rozszerzeniem drugiego, więc w myśl twierdzenia o sumie liniowych porządków( Zbiory uporządkowane pod koniec) relacja jest liniowym porządkiem na swoim polu, czyli na podzbiorze zbioru . Zatem Z własności sumy jest supremum względem inkluzji dla Zobacz ilustrację obok.
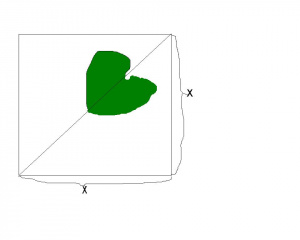
Niech będzie niepustym zbiorem. Rodzinę podzbiorów nazywamy rozkładem (podziałem) zbioru , gdy:
dla dowolnego
Czyli jest to rodzina zbiorów niepustych, których suma wynosi , i tak, że każde dwa różne zbiory tej rodziny są rozłączne, (czyli wtedy - ich przekrój jest zbiorem pustym). Intuicyjnie jest to dowolne pokrojenie zbioru na kawałki- zobacz ilustracje obok.
Dla dowolnego niepustego zbioru przykładem jego rozkładu może być rodzina wszystkich zbiorów jednoelementowych( co łatwo sprawdzić). Jest to "najdrobniejszy" rozkład zbioru . Przy okazji zauważmy (prawdziwy) fakt, że dla dowolnego rozkładu zbioru jego moc (ilość elementów ) jest co najwyżej taka jak moc zbioru .