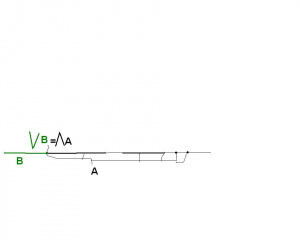Dalsze zagadnienia

Będę tu prezentował dodatkowe, raczej proste zadania( bo były fajne zadania, które zostawiłem na potem). Będą to raczej proste problemy.

Uzasadnimy najpierw, że dla dwóch rodzin zbiorów [math]\mathbb{X}, \mathbb{Y}[/math] nie zawsze zachodzi równość zbiorów:

[math]\bigcap\left( \mathbb{X} \cap \mathbb{Y}\right)= \bigcap \mathbb{X} \cap \bigcap \mathbb{Y}.[/math]

Jako kontrprzykład dla tej równości połóżmy [math]X=\left\{ 1,2\right\} [/math] [math]Y=\left\{ 2,3\right\}[/math] oraz [math]\mathbb{X}=\left\{ X\right\}, \mathbb{Y}=\left\{ Y\right\}.[/math]

Wtedy [math]\bigcap \mathbb{X}=X[/math], podobnie [math]\bigcap \mathbb{Y}=Y[/math], zatem [math]\bigcap \mathbb{X} \cap \bigcap \mathbb{Y}=X\cap Y=\left\{ 2\right\}.[/math]

Podczas gdy [math]\mathbb{X} \cap \mathbb{Y}=\emptyset[/math], bo zbiory [math]X\neq Y[/math], zatem [math]\bigcap\left( \mathbb{X} \cap \mathbb{Y}\right)=\bigcap\emptyset=\emptyset\neq\left\{ 2\right\}[/math], równość więc nie jest prawdą.

Zastanówmy się nad inkluzjami dla rodziny zbiorów [math]\mathbb{X}[/math]: [math]\bigcup\mathbb{X}\subset \mathbb{X}[/math], oraz [math]\bigcup\mathbb{X}\supset \mathbb{X}.[/math] Otóż, wbrew pozorom, ta ostatnia inkluzja jest o wiele bardziej nietypowa. Pierwsza inkluzja mówi, że elementy [math]\bigcup\mathbb{X}[/math] są elementami [math]\mathbb{X}[/math], czyli elementy elementów [math]\mathbb{X}[/math] (zbiorów rodziny [math]\mathbb{X}[/math]) są elementami [math]\mathbb{X}[/math]- są to tzw. zbiory(rodziny zbiorów) przechodnie. Równoważnie to możemy określić warunkiem [math]\mathbb{X}\subset P\left( \mathbb{X}\right)[/math], bo ten warunek oznacza, że zbiory rodziny [math]\mathbb{X}[/math] są elementami [math]P\left( \mathbb{X}\right)[/math], czyli są podzbiorami [math]\mathbb{X}[/math], w związku z czym ich elementy są elementami [math]\mathbb{X}[/math], czyli to oznacza, że elementy elementów [math]\mathbb{X}[/math] są elementami [math]\mathbb{X}[/math]. O takich zbiorach przechodnich będziemy jeszcze pisać.

Natomiast inkluzja [math]\bigcup\mathbb{X}\supset \mathbb{X}.[/math] jest o wiele dziwniejsza. Mówi ona, że zbiory rodziny [math]\mathbb{X}[/math] są elementami [math]\bigcup\mathbb{X}[/math], a więc elementów tych zbiorów. A to przecież elementy zbiorów rodziny [math]\mathbb{X}[/math] są elementami odpowiednich zbiorów. Jednak taka dziwaczna inkluzja jest możliwa. Niech [math]\mathbb{X}[/math] będzie dowolną rodziną induktywną (tzn. spełniającą aksjomat nieskończoności). Wykażemy, że wtedy [math]\bigcup\mathbb{X}\supset \mathbb{X}.[/math]

Niech [math]A\in\mathbb{X}.[/math] Pokażemy, że [math]A\in\bigcup\mathbb{X}.[/math] Ponieważ [math]\mathbb{X}[/math] jest zbiorem induktywnym, to [math]A'=A\cup\left\{ A\right\}\in\mathbb{X}[/math], ponieważ [math]A\in A\cup\left\{ A\right\}\in\mathbb{X}[/math], to [math]A\in\bigcup\mathbb{X}. \square[/math]

Zastanówmy się teraz uważnie nad pytaniem: Czy istnieje więcej niż jeden zbiór(rodzina zbiorów) [math]\mathbb{X}[/math] taka, że [math]\bigcap \mathbb{X} = \bigcup \mathbb{X}[/math]?

Otóż wiemy, że dla dowolnego zbioru [math]X[/math] mamy [math]\bigcap \left\{X\right\}=X=\bigcup \left\{X\right\},[/math] a więc istnieje przynajmniej jedna taka rodzina zbiorów. Biorąc teraz dwa różne zbiory [math]A,B[/math], zauważamy, że wtedy rodziny zbiorów [math]\left\{A\right\}, \left\{B\right\}[/math] są różne (bo zbiory [math]A,B[/math] są różne). Zgodnie z przytoczonym faktem [math]\bigcap \left\{A\right\}=A=\bigcup \left\{A\right\},[/math] oraz [math]\bigcap \left\{B\right\}=B=\bigcup \left\{B\right\}[/math], wobec czego istnieją co najmniej dwie rodziny zbiorów [math]\mathbb{X}[/math], takie,że iloczyn rodziny [math]\mathbb{X}[/math] jest równy sumie rodziny [math]\mathbb{X}[/math].

Dla dowolnego zbioru [math]X[/math], mamy: [math]\bigcup P\left( X\right)=X.[/math]

Dowód: Aby pokazać, że [math]\bigcup P\left( X\right)=X,[/math] pokazujemy dwa zawierania.

Inkluzja w prawo: Suma rodziny wszystkich podzbiorów [math]X[/math], a więc suma szczególnej rodziny podzbiorów [math]X[/math] musi być podzbiorem [math]X[/math].

Inkluzja w lewo: Wiemy,że suma dowolnej rodziny zbiorów jest nadzbiorem każdego zbioru tej rodziny, więc suma rodziny wszystkich podzbiorów [math]X[/math] jest nadzbiorem [math]X[/math] (bo [math]X \subset X[/math], a więc [math]X\in P\left( X\right)[/math]).

A więc [math]\bigcup P\left( X\right)=X.\square[/math]

Dla dowolnej rodziny zbiorów [math]\mathbb{X}[/math] mamy:

[math]\mathbb{X}\subset P\left( \bigcup \mathbb{X}\right).[/math]

Dowód: Niech [math]A\in\mathbb{X}[/math]. Skoro [math]A[/math] jest zbiorem z rodziny [math]\mathbb{X}[/math], to z własności sumy [math]A[/math] jest podzbiorem sumy tej rodziny, czyli [math]A\subset \bigcup \mathbb{X}.[/math] To z kolei oznacza, że [math]A\in P\left( \bigcup \mathbb{X}\right)[/math], i z dowolności [math]A[/math], otrzymujemy [math]\mathbb{X}\subset P\left( \bigcup \mathbb{X}\right).\square[/math]

Jednak inkluzja w drugą stronę nie zawsze zachodzi. Kontrprzykładem będzie rodzina [math]\mathbb{X}= \{\{\emptyset\}\}.[/math] Wtedy:

[math]\mathcal{P}(\bigcup\{\{\emptyset\}\} \ \ )= \mathcal{P}(\{\emptyset\}) = \{\emptyset,\{\emptyset\}\}\neq \{\{\emptyset\}\}=\mathbb{X},[/math] bo [math]\emptyset\notin \{\{\emptyset\}\}[/math], bo [math]\emptyset\neq \{\emptyset\}.[/math] Zatem tutaj [math]\mathbb{X}\neq P\left( \bigcup \mathbb{X}\right).[/math]

Jeśli mamy funkcję [math]f:X\rightarrow X[/math], to element [math]x\in X[/math] nazywamy punktem stałym funkcji [math]f[/math], gdy [math]f(x)=x.[/math]

Niech [math]X[/math] będzie zbiorem. Rozważmy funkcję [math]f:P\left( P\left( X\right) \right) \rightarrow P\left( P\left( X\right) \right),[/math] określoną jako:

[math]f\left( x\right)=\left\{ \bigcup x, \bigcap x\right\} .[/math]

Czyli funkcja [math]f[/math] dostaje jako argument rodzinę podzbiorów [math]X[/math], i przypisuje jej rodzinę złożoną z dwóch zbiorów- zbioru będącego sumą tej rodziny oraz zbioru będącego iloczynem tej rodziny. Podamy kilka przykładów punktów stałych dla tej funkcji.

Dla dowolnego zbioru [math]A\subset X[/math], mamy [math]f\left( \left\{ A\right\} \right)=\left\{ \bigcup \left\{ A\right\} , \bigcap \left\{ A\right\} \right\}=\left\{ A,A\right\} =\left\{ A\right\} .[/math] A więc rodzina [math]\left\{ A\right\}[/math] jest punktem stałym. Kolejne przykłady:

Dla dowolnego zbioru [math]A \subset X[/math], mamy [math]f\left( \left\{ A,\emptyset \right\} \right)=\left\{ \bigcup\left\{ A,\emptyset \right\}, \bigcap\left\{ A,\emptyset \right\} \right\}=\left\{ A \cup \emptyset, A \cap \emptyset \right\}=\left\{ A,\emptyset \right\}.[/math]

Dla dowolnych zbiorów [math]A,B \subset X[/math], takich, że [math]A \subset B[/math] mamy: [math]f\left( \left\{ A,B\right\} \right)=\left\{ A \cup B, A \cap B\right\}=\left\{ B,A\right\}=\left\{ A,B\right\},[/math] gdzie przedostatnia równość pochodzi z założenia, że [math]A \subset B.[/math]

Zwróćmy uwagę, że istnieją funkcje, które nie mają punktów stałych. Prostym przykładem może być funkcja [math]f:\left\{ 0,1\right\} \rightarrow \left\{ 0,1\right\},[/math] daną jako [math]f=\left\{ \left( 0,1\right),\left( 1,0\right) \right\}.[/math]

Kolejny przykład. Niech [math]X[/math] będzie niepustym zbiorem. Wykażemy, że dla funkcji [math]f:P\left( X\right) \rightarrow P\left( X\right),[/math] określonej jako [math]f\left( A\right)=X \setminus A[/math], nie istnieje punkt stały.

Przypuśćmy, że istnieje punkt stały, nazwijmy go [math]A[/math]. Wtedy [math]f\left( A\right)=A.[/math] Z drugiej strony, z definicji tej funkcji mamy [math]f\left( A\right)=X \setminus A.[/math] Wnioskujemy, że [math]A=X \setminus A.[/math] Ponieważ zbiór [math]X[/math] jest niepusty, więc istnieje element [math]x \in X,[/math] ustalamy taki element. Rozstrzygnijmy problem czy [math]x \in A.[/math] Jeśli tak, to z tej równości wynika, że [math]x \in X \setminus A[/math], a więc z definicji różnicy zbiorów [math]x \notin A[/math]- sprzeczność. Jeśli [math]x\notin A[/math], to [math]x \in X \setminus A,[/math] a więc z tej równości wynika, że [math]x \in A[/math], i również otrzymujemy sprzeczność, co kończy ten prosty dowód.[math]\square[/math]

Dla funkcji [math]f:P\left( X\right) \rightarrow P\left( X\right),[/math] zbiór [math]A \subset X[/math] nazywamy najmniejszym punktem stałym, gdy [math]f\left( A\right)=A,[/math] (czyli [math]A[/math] jest punktem stałym) oraz dla dowolnego zbioru [math]B \subset X[/math] spełniony jest warunek [math]f\left( B\right)=B \rightarrow A \subset B.[/math] Czyli gdy każdy punkt stały [math]B[/math] jest większy pod względem inkluzji od [math]A[/math]- od tego najmniejszego punktu stałego, czyli zbiór [math]B[/math] jest nadzbiorem zbioru [math]A[/math].

Podobnie dla funkcji [math]f:P\left( X\right) \rightarrow P\left( X\right),[/math] zbiór [math]A \subset X[/math] nazwiemy największym punktem stałym, gdy jest punktem stałym, oraz każdy zbiór [math]B \subset X[/math] będący punktem stałym jest podzbiorem [math]A[/math], czyli wtedy zbiór [math]A[/math] jest większy pod względem inkluzji od [math]B[/math].

Poniższy przykład pokazuje, że dla funkcji może się zdarzyć, że mimo, że istnieją punkty stałe, ale nie istnieje największy punkt stały.

Niech [math]X[/math] będzie niepustym zbiorem. Rozważmy funkcję [math]f:P\left( P\left( X\right) \right) \rightarrow P\left( P\left( X\right) \right)[/math], określoną jako [math]f\left( \mathbb{A}\right)= \left\{ \bigcup \mathbb{A} \right\},[/math] czyli funkcja [math]f[/math] dostaje jako argument rodzinę podzbiorów [math]X[/math], i przypisuje jej zbiór jednoelementowy złożony z sumy tej rodziny. Jeśli [math]\mathbb{A}[/math] jest rodziną podzbiorów [math]X[/math], która jest punktem stałym, to wtedy [math]f\left( \mathbb{A}\right)=\mathbb{A}= \left\{ \bigcup \mathbb{A} \right\}.[/math] Widać więc, że punktami stałymi mogą być tylko rodziny jednozbiorowe (jednoelementowe)- bo zbiór [math]\left\{ \bigcup \mathbb{A} \right\}[/math] jest jednoelementowy. Wykażemy teraz, że każda rodzina jednozbiorowa jest punktem stałym. Niech [math]A \subset X.[/math] Pokazujemy, że [math]\left\{ A\right\}[/math] jest punktem stałym. Z określenia funkcji mamy [math]f\left( \left\{ A\right\} \right)= \left\{ \bigcup \left\{ A\right\} \right\}=\left\{ A\right\}.[/math] Zatem [math]\left\{ A\right\}[/math] jest punktem stałym. Zatem dla tej funkcji punktami stałymi są dokładnie rodziny jednozbiorowe. Ponieważ [math]X[/math] jest niepusty, więc ma co najmniej dwa różne podzbiory [math]A,B[/math] (np. [math]\emptyset[/math] i [math]X[/math]). Ustalmy dwa takie różne podzbiory [math]A,B.[/math] Wtedy rodziny zbiorów [math]\left\{ A\right\},\left\{ B\right\}[/math] są różne ( bo zbiory [math]A,B[/math] są różne). Zgodnie z udowodnioną własnością rodziny zbiorów [math]\left\{ A\right\},\left\{ B\right\}[/math] są punktami stałymi. Gdyby istniał tu największy punkt stały, to musiałby być nadzbiorem [math]\left\{ A\right\}[/math] oraz [math]\left\{ B\right\},[/math] zatem musiałby mieć co najmniej dwa elementy ([math]A,B[/math]). A ponieważ jest to punkt stały, i punktami stałymi są dokładnie rodziny jednozbiorowe otrzymujemy sprzeczność. Wobec czego tu nie istnieje największy punkt stały ( choć istnieją co najmniej dwa punkty stałe).

Jednak każda funkcja [math]f:P\left( X\right) \rightarrow P\left( X\right)[/math], która jest monotoniczna ze względu na inkluzję, posiada najmniejszy punkt stały oraz ma największy punkt stały.

Monotoniczna pod względem inkluzji, tzn. spełnia warunek dla dowolnych zbiorów [math]A,B \subset X[/math]:

[math]A \subset B \rightarrow f\left( A\right) \subset f\left( B\right).[/math]

Warunek ten mówi, że jeśli na argumentach funkcji zachodzi inkluzja (przypominamy,że argumentami i wartościami funkcji są tu podzbiory zbioru [math]X[/math]), to na odpowiadających im wartościach również zachodzi (zgodna) inkluzja. Funkcję monotoniczne ze względu na inkluzję zachowują relację inkluzji pomiędzy przekształcanymi zbiorami.

Ilustracja funkcji za pomocą grafu

Przypomnijmy intuicję ze szkoły, że funkcja pomiędzy dwoma zbiorami, to przyporządkowanie każdemu elementowi pierwszego zbioru dokładnie jednego elementu drugiego zbioru. U nas rolę przyporządkowania w sposób ścisły pełni relacja pomiędzy tymi zbiorami. Każda funkcja jest zatem zbiorem par uporządkowanych. Spróbujemy jednak zilustrować funkcję za pomocą grafu. Wiemy, że funkcja jest zbiorem par, a każdy zbiór jest (sam w sobie) nieuporządkowany. Możemy zatem te pary ustawić w takiej kolejności jak chcemy. Weźmy element dziedziny [math]x \in X[/math], z definicji funkcji jest mu przypisany dokładnie jeden element [math]y\in Y[/math]. Łączymy te elementy, łączymy wszystkie elementy dziedziny którym jest przypisana wartość [math]y[/math] z elementem [math]y[/math]. Bierzemy kolejny inny element dziedziny funkcji [math]x _{1}[/math], przypisany jest mu jeden element [math]y _{1}[/math]. Łączymy te elementy, łączymy wszystkie elementy dziedziny którym jest przypisana wartość [math]y_{1}[/math] z elementem [math]y _{1}[/math]. Bierzemy kolejny inny element dziedziny funkcji [math]x _{2}[/math], robimy ten proces aż się wyczerpią elementy dziedziny(u nas cztery serie- zobacz ilustrację obok).

Jeśli funkcja [math]f:X \rightarrow Y[/math] jest bijekcją, to relacja odwrotna [math]f ^{-1}[/math] jest funkcją bijekcją ze zbioru [math]Y[/math] w zbiór [math]X[/math].

Dowód:

Pokażemy, że [math]\left( f ^{-1}\right) _{L}=Y.[/math] Niech [math]y\in Y.[/math] Ponieważ [math]f[/math] jest bijekcją, to jest 'na' zbiór [math]Y[/math], więc [math]y=f \left( x\right) ,[/math] przy pewnym [math]x\in X[/math]. Inaczej mówiąc [math]\left( x,y\right) \in f[/math]. Wtedy z określenia relacji odwrotnej [math](y,x)\in f^{-1}[/math], a więc [math]y[/math] należy do [math]\left( f ^{-1}\right) _{L}[/math]. Wobec dowolności wyboru [math]y[/math] otrzymujemy [math]\left( f ^{-1}\right) _{L}=Y.[/math]

Pokażemy, że relacja [math]f ^{-1}[/math] jest funkcją ze zbioru [math]Y[/math] w zbiór [math]X[/math]. Przypuśćmy dla dowodu nie wprost, że nie jest funkcją. Oznacza to, że istnieje element [math]y\in Y[/math] oraz elementy [math]x_1,x_2\in X[/math] takie, że [math]x_1 \neq x_2, \left( y, x_{1} \right) \in f^{-1}[/math], i [math]\left( y, x_{2} \right) \in f^{-1}.[/math] Wtedy [math]\left( x _{1},y \right) \in f[/math] i [math]\left( x _{2},y \right) \in f[/math] inaczej mówiąc [math]f\left( x _{1} \right)=y= f\left( x _{2}\right),[/math] i ponieważ [math]f[/math] jest bijekcją, więc jest różnowartościowa, więc otrzymujemy sprzeczność wobec tego, że ta funkcja różnym elementom [math]x_{1}, x_{2}[/math] przypisuje tą samą wartość [math]y.[/math]

Pokażemy, że funkcja [math]f ^{-1}[/math] jest funkcją różnowartościową. Weźmy dowolne pary należące do niej [math]\left( y _{1},x\right),\left( y _{2},x\right),[/math] które mają taką samą drugą współrzędną [math]x[/math]. Pokażemy, że [math]y_1=y_2.[/math] Ponieważ [math]\left( y _{1},x\right),\left( y _{2},x\right) \in f^{-1},[/math] to [math]\left(x, y_{1} \right) \in f[/math] i [math]\left(x, y_{2} \right) \in f[/math], wobec czego, i ponieważ [math]f[/math] jest funkcją, otrzymujemy [math]y_1=y_2[/math]. Zatem [math]f ^{-1}[/math] jest funkcją różnowartościową.

Pokażemy, że funkcja [math]f ^{-1}[/math] jest 'na' zbiór [math]X[/math]. Niech [math]x\in X[/math]. Ponieważ [math]f:X \rightarrow Y[/math], to istnieje jedyny element [math]y \in Y[/math], taki, że [math]f\left( x\right)=y.[/math] Inaczej mówiąc [math]\left( x,y\right) \in f[/math], a więc [math]\left( y,x\right) \in f^ {-1}[/math] , inaczej mówiąc [math]f^{-1} \left( y\right)=x[/math], a więc [math]x[/math] jest wartością funkcji [math]f^{-1}.[/math] Wobec dowolności [math]x\in X[/math] ,funkcja [math]f^{-1}[/math] jest 'na' zbiór [math]X.[/math]

Zatem [math]f ^{-1}[/math] jest funkcją bijekcją ze zbioru [math]Y[/math] w zbiór [math]X. \square[/math]

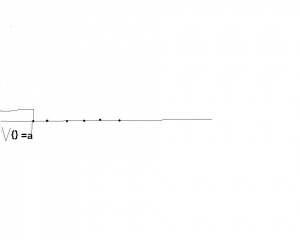
Wykażemy, że jeśli w zbiorze uporządkowanym [math]\left( X, \le \right)[/math] jest element najmniejszy, to jest on supremum zbioru pustego, ( pustego podzbioru [math]X[/math]). Zobacz ilustrację obok.

Niech [math]a[/math] będzie elementem najmniejszym w [math]X[/math]. Pokażemy, że [math]a[/math] spełnia warunki bycia supremum [math]\bigvee \left\{ \right\} .[/math]

1. Należy pokazać, że [math]a[/math] jest ograniczeniem górnym zbioru pustego, czyli [math]b\le a[/math] dla dowolnego [math]b\in\left\{ \right\}[/math], oczywiście jest to (formalnie) prawda.

2. Niech [math]b[/math] będzie ograniczeniem górnym zbioru pustego. Ponieważ [math]a[/math] jest elementem najmniejszym, to natychmiast otrzymujemy, że [math]a \le b[/math]. Wobec dowolności [math]b[/math] oznacza, to że [math]\bigvee \left\{ \right\}=a .\square[/math]

W sposób symetryczny można pokazać, że jeśli w zbiorze uporządkowanym [math]\left( X, \le \right)[/math] jest element największy, to jest on infimum zbioru pustego, ( pustego podzbioru [math]X[/math]).

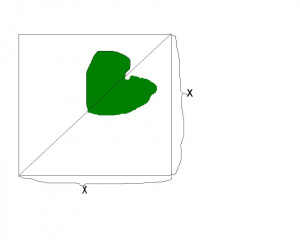
W zbiorze uporządkowanym jeśli każdy podzbiór ma supremum, to każdy podzbiór ma infimum.

Przedstawmy jedynie piękny szkic dowodu.

Niech [math]\left( X, \le \right)[/math] będzie zbiorem uporządkowanym w którym każdy podzbiór ma supremum. Należy pokazać, że każdy podzbiór ma infimum. Weźmy zbiór [math]A\subset X[/math]. Należy pokazać, że [math]A[/math] ma infimum. Rozważmy zbiór [math]B[/math] na lewo od zbioru [math]A[/math]( czyli zbiór ograniczeń dolnych zbioru [math]A[/math]). Taki zbiór [math]B[/math] jako podzbiór [math]X[/math] ma supremum, i pokazujemy, że to supremum jest infimum zbioru [math]A[/math] na prawo. Zobacz ilustrację obok.

W sposób symetryczny, w zbiorze uporządkowanym, jeśli każdy podzbiór ma infimum, to każdy podzbiór ma supremum.

Symetrycznie- trzeba wziąć zbiór [math]A\subset X[/math], i rozważyć zbiór na prawo od niego. Taki zbiór ma infimum, i pokazujemy, że to infimum jest supremum zbioru na lewo- zbioru [math]A[/math].

Niech [math]X[/math] będzie zbiorem. Wtedy rodzina jego wszystkich podzbiorów [math]P \left( X\right)[/math] jest uporządkowana przez inkluzję, zatem [math]\left( P\left( X\right), \subset \right)[/math] jest zbiorem uporządkowanym. Wtedy mówiliśmy, że dla dowolnej rodziny [math]\mathbb{A} \subset P\left( X\right)[/math], mamy [math]\bigvee \mathbb{A}= \bigcup\mathbb{A},[/math] a jeśli dodatkowo rodzina [math]\mathbb{A}[/math] jest niepusta, to [math]\bigwedge \mathbb{A}= \bigcap\mathbb{A}.[/math] Objaśniając, jeśli weźmiemy rodzinę [math]\mathbb{A}[/math] podzbiorów [math]X[/math], wtedy supremum tej rodziny jest suma tej rodziny, a jeśli dodatkowo rodzina jest niepusta, to jej infimum to iloczyn tej rodziny. Dla pustej rodziny, mamy, jej infimum to element największy( mówiliśmy, że element największy jest infimum zbioru pustego), czyli tutaj cały zbiór [math]X[/math]( jest największym elementem [math]P\left( X\right)[/math] pod względem inkluzji), podczas gdy [math]\bigcap\emptyset=\emptyset.[/math] Równość więc dla niepustego zbioru [math]X[/math] nie ma miejsca.

Ilustracja relacji zwrotnej

Relacja [math]R[/math] w zbiorze [math]X[/math] jest zwrotna dokładnie wtedy, gdy zawiera relację identyczności na [math]X[/math]. Zilustrujmy to lepiej- zobacz obok.

Relacja [math]R \subset X \times X[/math] jest symetryczna, jeśli spełnia warunek (dla dowolnych [math]x,y \in X[/math])

[math]\left( x,y\right)\in R \rightarrow \left( y,x\right) \in R.[/math]

Czyli jeśli elementy [math]x,y[/math] są ze sobą w relacji [math]R[/math], to symetrycznie [math]y,x[/math] są również w relacji [math]R[/math].

Przykład: Niech [math]X=\left\{ 0,1\right\}.[/math] [math]R=\left\{ \left( 0,1\right), \left(1,0 \right) \right\}[/math] Taka relacja jest symetryczna. Niech [math]S=\left\{ \left( 0,0\right) ,\left( 0,1\right) \right\}[/math] Natomiast relacja [math]S[/math] nie jest symetryczna, bo [math]\left( 0,1\right) \in S[/math], podczas gdy [math]\left( 1,0\right) \notin S.[/math]

Relacja symetryczna jest symetryczna względem przekątnej- zobacz ilustrację obok.

Niech [math]X[/math] będzie zbiorem, a [math]R[/math] relacją w tym zbiorze. Wtedy poniższe warunki są równoważne.

(1) [math]R[/math] jest symetryczna,

(2) [math]R=R ^{-1}.[/math]

Czyli [math]R[/math] jest symetryczna, równoważnie gdy jest równa swojej relacji odwrotnej.

Dowód:

[math](1) \rightarrow (2)[/math] Załóżmy, że [math]R[/math] jest symetryczna. Aby pokazać, że [math]R=R ^{-1},[/math] pokazujemy dwie inkluzję. Inkluzja w prawo: [math]R \subset R ^{-1}.[/math] Niech [math]\left( x,y\right) \in R.[/math] Wtedy ponieważ [math]R[/math] jest symetryczna, więc [math]\left( y,x\right) \in R,[/math] a więc z określenia relacji odwrotnej [math]\left( x,y\right) \in R ^{-1}.[/math] Zatem [math]R \subset R ^{-1}.[/math] Inkluzja w lewo: [math]R \supset R ^{-1}.[/math] Niech [math]\left( x,y\right) \in R ^{-1}.[/math] Wtedy z określenia relacji odwrotnej [math]\left( y,x\right) \in R.[/math] Ponieważ [math]R[/math] jest symetryczna, więc również [math]\left( x,y\right) \in R.[/math] Zatem [math]R \supset R ^{-1},[/math] i [math]R=R ^{-1}.[/math]

[math](2) \rightarrow (1)[/math] Załóżmy, że [math]R=R ^{-1}.[/math] Aby pokazać, że [math]R[/math] jest symetryczna, to niech [math]\left( x,y\right) \in R.[/math] Wtedy z założonej równości [math]\left( x,y\right) \in R ^{-1},[/math] a więc z określenia relacji odwrotnej [math]\left( y,x\right) \in R.[/math] Wnioskujemy, że [math]R[/math] jest symetryczna.[math]\square[/math]

Jako przykład zastosowania tego twierdzenia, wykażemy, że suma dwóch relacji symetrycznych na tym samym zbiorze jest relacją symetryczną.

Niech [math]X[/math] będzie zbiorem, a [math]R,S[/math] relacjami symetrycznymi w zbiorze [math]X[/math]. Wykażemy, że relacja [math]R \cup S[/math] jest relacją symetryczną.

Dowód:

Ponieważ [math]R,S[/math] są relacjami symetrycznymi, więc [math]R= R^{-1}[/math], i [math]S= S^{-1}.[/math] Wobec czego:

[math]\left( R \cup S\right) ^{-1}= R^{-1}\cup S^{-1}=R \cup S,[/math] czyli [math]\left( R \cup S\right) ^{-1}=R \cup S,[/math] a więc relacja [math]R \cup S[/math] jest symetryczna.[math]\square[/math]

Wykażemy, że w każdym niepustym skończonym podzbiorze [math]A\subset X[/math] liniowo uporządkowanego zbioru [math]\left( X,\le\right)[/math] jest element najmniejszy i największy.

Niech [math]\left( X, \le \right)[/math] będzie zbiorem liniowo uporządkowanym, a [math]A \subset X[/math] niepustym skończonym podzbiorem. Wykażemy, że w [math]A[/math] jest element najmniejszy i największy. Dowód poprowadzimy indukcyjnie ze względu na ilość elementów zbioru [math]A[/math].

Jeśli [math]A[/math] jest jednoelementowy, tzn. [math]A=\left\{ a\right\}[/math], to wtedy ten element [math]a[/math] jest jego elementem najmniejszym i największym.

Przypuśćmy, że twierdzenie zachodzi dla zbiorów [math]n[/math]-elementowych ([math]n \ge 1[/math]). Weźmy dowolny ([math]n+1[/math])-elementowy zbiór [math]A \subset X[/math]. Ustalmy [math]a\in A[/math]. Rozważmy [math]A \setminus\left\{ a\right\}[/math] jest to zbiór [math]n[/math]-elementowy, zatem możemy zastosować do niego założenie indukcyjne, i dostać jego element najmniejszy [math]b[/math] i największy [math]B[/math]. Wtedy ponieważ jesteśmy na zbiorze liniowo uporządkowanym, więc elementy [math]b[/math] i [math]a[/math] są porównywalne, i wtedy mniejszy z elementów [math]b[/math] i [math]a[/math] jest elementem najmniejszym [math]A[/math]( bo [math]b[/math] jest najmniejszy w [math]A \setminus\left\{ a\right\}[/math] ). Podobnie, większy z elementów [math]B[/math] i [math]a[/math] jest elementem największym [math]A[/math]. Dowolność zbioru [math]A[/math] kończy dowód kroku indukcyjnego, i cały dowód.[math]\square[/math]