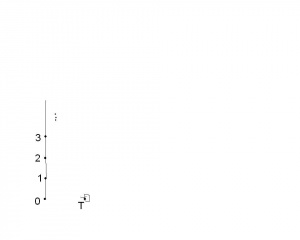Zbiory uporządkowane: Różnice pomiędzy wersjami
(→Łańcuchy i antyłańcuchy) |
(→Diagramy Hassego) |
||
| Linia 124: | Linia 124: | ||
== Diagramy Hassego == | == Diagramy Hassego == | ||
| − | [[Plik:Diagram_Hassego.JPG|300px|thumb|right|Przykład diagramu Hassego]] | + | [[Plik:Diagram_Hassego.JPG|300px|thumb|right|Przykład diagramu Hassego]] [[Plik:Diagram_Hassego-_element_najmniejszy_i_najw..JPG|300px|thumb|left|]] |
Skończone zbiory uporządkowane wygodnie jest czasem przedstawiać na grafach, tzw. | Skończone zbiory uporządkowane wygodnie jest czasem przedstawiać na grafach, tzw. | ||
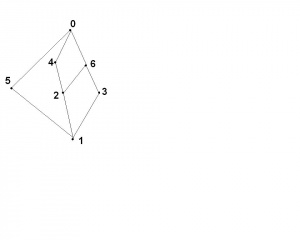
| − | '''diagramach Hassego.''' Zobacz ilustrację obok. Odczytujemy,że '''w tym''' zbiorze uporządkowanym <math>3<4,4<5,3<5,2<1,4<6,3<6.</math> Ogólnie, element <math>x</math> jest mniejszy od elementu <math>y</math>, jeśli element <math>x</math> można połączyć drogą z elementem <math>y</math>, idąc cały czas w górę( bądź na ukos). Dlatego '''tutaj''' <math>2\not<3,4,5,6.</math> | + | '''diagramach Hassego.''' Zobacz ilustrację obok na prawo. Odczytujemy,że '''w tym''' zbiorze uporządkowanym <math>3<4,4<5,3<5,2<1,4<6,3<6.</math> Ogólnie, element <math>x</math> jest mniejszy od elementu <math>y</math>, jeśli element <math>x</math> można połączyć drogą z elementem <math>y</math>, idąc cały czas w górę( bądź na ukos). Dlatego '''tutaj''' <math>2\not<3,4,5,6.</math> |
| − | + | ||
Na diagramie Hassego odczytujemy, że element jest najmniejszy, kiedy wszystkie elementy na tym diagramie dochodzą do niego (w dół). Podobnie odczytujemy element największy (tylko w górę). Zobacz ilustrację obok- tu <math>1</math> jest elementem najmniejszym, a <math>0</math> jest elementem największym- jest to diagram Hassego dla relacji podzielności na zbiorze <math>\{ 0,1,2,3,4,5,6\}.</math> | Na diagramie Hassego odczytujemy, że element jest najmniejszy, kiedy wszystkie elementy na tym diagramie dochodzą do niego (w dół). Podobnie odczytujemy element największy (tylko w górę). Zobacz ilustrację obok- tu <math>1</math> jest elementem najmniejszym, a <math>0</math> jest elementem największym- jest to diagram Hassego dla relacji podzielności na zbiorze <math>\{ 0,1,2,3,4,5,6\}.</math> | ||
Aktualna wersja na dzień 00:51, 22 lis 2018
Zbiorem uporządkowanym (częściowo) nazywamy parę , gdzie jest zbiorem, a jest relacją:
1. Zwrotną, tzn. dla dowolnego zachodzi
2. Antysymetryczną, tzn. spełnia warunek
3. Przechodnią, tzn. spełnia warunek
Jeżeli dodatkowo relacja jest spójna, tzn. dla dowolnych zachodzi lub , to wtedy parę , nazywamy zbiorem liniowo uporządkowanym. Mówimy wtedy, że jest liniowym porządkiem na , oraz że zbiór jest liniowo uporządkowany przez . Podobnie dla zbioru uporządkowanego, relację nazywamy porządkiem (częściowym) na zbiorze
Często oznaczamy relację porządku przez ( lub symbolami podobnymi np.). Dla zbioru uporządkowanego , dla dowolnego zachodzi bo relacja porządku jest zwrotna. Zatem dla elementów , oznaczamy gdy i i mówimy, że jest silnie mniejszy od Podobnie dla innych oznaczeń relacji porządku. W zbiorze uporządkowanym , będziemy czasem pisać zamiast , oraz zamiast
Warto zobaczyć jaką postać przyjmują wymagania stawiane zbiorom liniowo uporządkowanym, gdy relację liniowego porządku oznaczymy przez , (i gdy będziemy pisać zamiast będziemy pisać O zwrotności już pisałem, jako , dla dowolnego Antysymetria przyjmuję postać: jeżeli i , to . Przechodniość przyjmuję postać: jeżeli i , to Spójność zapisujemy jako: dla dowolnych ma zachodzić lub . Nietrudno więc zauważyć, że te własności są spełnione w zbiorach liczbowych z naturalnym porządkiem. Nasza definicja zbioru liniowego uporządkowanego jest więc uogólnieniem znanych własności porządkowych na zbiorach liczbowych. Nie zapominajmy jednak, że formalnie jest to zbiór wraz z relacją, która ma dokładnie wymienione własności.
Uwaga. Zbiór pusty jest liniowo uporządkowany przez relację pustą. Wynika to z faktu, ze własności zwrotności, antysymetrii, przechodniośći i spójności mają być spełnione dla dowolnych elementów zbioru uporządkowanego, czyli w tym wypadku zbioru pustego- a każde zdanie postaci jest prawdą
Niech będzie zbiorem uporządkowanym. niech . Element nazywamy elementem najmniejszym zbioru względem porządku , gdy , oraz gdy dla dowolnego , zachodzi
Tzn. element najmniejszy zbioru , to taki element , który jest mniejszy lub równy (względem rozpatrywanego porządku) od każdego elementu tego zbioru .
Analogicznie możemy zdefiniować element największy zbioru , jako taki element , który jest większy lub równy od każdego elementu tego zbioru, tzn. dla dowolnego zachodzi
Fakt 0. Jeśli w zbiorze uporządkowanym podzbiór ma element najmniejszy/ największy, to jest on jedynym elementem najmniejszym/największym w .
Dowód:
Przypuśćmy, że są elementami najmniejszymi w . Pokażemy, że . Elementy najmniejsze w należą do - . Ponieważ jednak jest elementem najmniejszym , to jest on mniejszy od każdego elementu w tym zbiorze, więc również . Podobnie, ponieważ jest elementem najmniejszym , to podobnie Ponieważ i to z antysymetrii porządku Dowód dla elementów największych jest analogiczny.
Przykład: Rozważmy zbiór liczb naturalnych uporządkowany ( to należy pokazać) relacją podzielności |, tzn.
Równoważnie to oznacza, że (dla ) iloraz jest pewną liczbą naturalną . Wykażemy, że jest zbiorem uporządkowanym, a potem, że jest elementem największym, a jest elementem najmniejszym (tak przekornie wychodzi- ale nie względem naturalnego porządku, tylko względem naszego porządku ).
Zwrotność. Niech Wtedy możemy dobrać , i otrzymać , a więc . Relacja jest więc zwrotna (zwróć uwagę co się dzieje dla , jak działa to proste rozumowanie).
Przechodniość. Niech będą takie, że oraz, że . Pokażemy, że . Nasze założenia oznaczają, że dla pewnej liczby naturalnej , oraz, że dla pewnej liczby naturalnej . Wobec czego Ponieważ iloczyn dwóch liczb naturalnych jest liczbą naturalną, więc możemy dobrać , tak aby , a więc
Antysymetria. Weźmy dowolne liczby naturalne , dla których i Nasze założenia oznaczają, że dla pewnej liczby naturalnej , oraz, że dla pewnej liczby naturalnej Wobec czego
Rozważymy teraz dwa przypadki. Jeśli , to wtedy , a więc z prawa skreśleń dla liczb naturalnych otrzymujemy, że , i ponieważ są to liczby naturalne, to , a więc , czyli .
Jeśli , to wtedy , czyli , więc Relacja jest więc antysymetryczna.
Zatem jest zbiorem uporządkowanym. W tym zbiorze uporządkowanym elementem największym jest , a najmniejszym .
Niech . Wtedy możemy dobrać , i otrzymać , a więc . Ponieważ każda liczba naturalna dzieli (czyli każda liczba naturalna jest mniejsza, względem relacji podzielności, od ), to jest elementem największym (względem - relacji podzielności.) W tym zbiorze uporządkowanym jest elementem najmniejszym. Niech . Wtedy możemy dobrać , i otrzymać , a więc . Ponieważ dzieli każdą liczbę naturalną (czyli jest mniejszy, względem relacji podzielności, od każdej liczby), to jest elementem najmniejszym.
Kolejny przykład. Niech będzie niepustym ustalonym zbiorem. Niech będą takie, że Niech . W zbiorze funkcji z do , czyli , wprowadzamy relację :
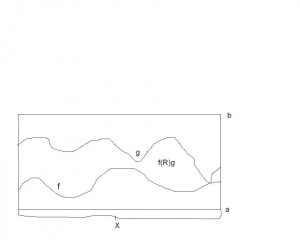
Wykażemy, że jest relacją porządku na . Geometrycznie ten porządek oznacza, że funkcja jest mniejsza od funkcji , gdy wykres funkcji w każdym punkcie leży poniżej (lub na równi) niż wykres funkcji (zobacz ilustrację obok).
Zwrotność. Niech . Niech . Wtedy niewątpliwie , a więc ze zwrotności naturalnego porządku na liczbach rzeczywistych , Z dowolności wyboru , oznacza to, że . Relacja jest więc zwrotna.
Antysymetria. Załóżmy, że i . Zatem dla dowolnego mamy oraz dla każdego , mamy Niech Wtedy oraz Z antysymetrii naturalnego porządku na liczbach rzeczywistych, otrzymujemy, że , Z dowolności wyboru , oznacza to, że . Relacja jest więc antysymetryczna.
Przechodniość. Załóżmy, że i . Zatem dla dowolnego mamy oraz dla każdego , mamy Niech Wtedy oraz Z przechodniości porządku otrzymujemy, że , Z dowolności wyboru , oznacza to, że . Relacja jest więc przechodnia.
Zatem jest zbiorem uporządkowanym. Elementem najmniejszym jest funkcja stale równa , a elementem największym funkcja stale równa , tzn.
Mamy bowiem, dla dowolnej funkcji z do , oraz dla dowolnego (bo są to funkcje o wartościach w ), mamy , a więc , zatem ( z dowolności ) , oraz , czyli jest elementem najmniejszym, oraz jest elementem największym.
Jeśli jest zbiorem uporządkowanym, a dla elementów , zachodzi lub , to mówimy, że elementy są porównywalne. W zbiorze liniowo uporządkowanym, każde więc dwa elementy są porównywalne. Jednak ogólniej, tzn. w zbiorze uporządkowanym tak być nie musi. Przyjęło się przyjmować w teorii mnogości, że zbiór jest uporządkowany, jeśli tylko niektóre jego elementy dadzą się porównać (np. każdy element jest porównywalny z samym sobą- na mocy zwrotności porządku). Istnieje bowiem wiele zbiorów, wraz z relacją, która jest relacją porządku na tym zbiorze, ale nie jest liniowym porządkiem na tym zbiorze (bo nie jest spójna). Rzeczywiście, poprzednie dwa przykłady o tym świadczą. Nie będę mówił, że naturalnym jest, że relacja podzielności jest porządkiem na . Ale zobacz ciekawy przykład drugi- zbiór funkcji. Co więcej, naturalnym jest dla mnie (i nie tylko), że zbiory mogą być mniejsze lub większe pod względem inkluzji. I okazuję się właśnie, że dla ustalonego zbioru , jego zbiór potęgowy (czyli zbiór jego wszystkich podzbiorów) jest uporządkowany przez inkluzję, ale niekoniecznie liniowo. Zbiory mogą być nieporównywalne przez inkluzję. Jest to zatem, nie jeden przykład na to, lecz cała rodzina przykładów. Pokażemy nawet jeszcze więcej.
Twierdzenie 1. Niech będzie dowolnym ustalonym zbiorem, i niech ( czyli jest zbiorem niektórych podzbiorów ). Zdefiniujmy relację na zbiorze :
Wykażemy, że jest zbiorem uporządkowanym.
Dowód:
Zwrotność. Dla dowolnego zbioru , mamy . więc również dla elementów , mamy , a więc . Relacja jest więc zwrotna.
Przechodniość. Weźmy dowolne zbiory , dla których i . Oznacza to, że i . Daje to , a więc . Relacja jest więc przechodnia.
Antysymetria. Weźmy dowolne zbiory , dla których i . Oznacza to, że i . Daje to . Antysymetria jest więc pokazana.
Zatem jest zbiorem uporządkowanym. Jest to jednak niekoniecznie liniowo zbiór uporządkowany. Kontrprzykładem będzie: , , , . Wtedy oraz
Będziemy używać symbolu dla oznaczenia relacji zdefiniowanej w poprzednim twierdzeniu. Zwracamy przy tym uwagę, że nie ma czegoś takiego jak relacja , gdyż musiałaby ona być określona pomiędzy dwoma dowolnymi zbiorami, a więc w zbiorze wszystkich zbiorów, który nie istnieje. W przypadku jednak, gdy rozważamy jedynie podzbiory ustalonego zbioru , możemy mówić o relacji bycia podzbiorem.
Spis treści
Elementy maksymalne i minimalne
Niech będzie zbiorem uporządkowanym. Element nazywamy maksymalnym, gdy dla dowolnego zachodzi:
Tzn. element jest maksymalny, gdy jeśli jest większy lub równy od - elementu maksymalnego, to musi ten być równy temu elementowi maksymalnemu, a więc nie ma elementów silnie większych od elementu maksymalnego. Podobnie definiujemy elementy minimalne.
W zbiorze uporządkowanym , element nazywamy elementem minimalnym, gdy dla dowolnego zachodzi:
Tzn. element jest minimalny, gdy nie ma silnie mniejszych od niego elementów, a więc gdy element jest słabo mniejszy od elementu minimalnego, to musi być mu równy.
Przykład. Podamy przykład zbioru uporządkowanego, w którym istnieje element maksymalny, który nie jest elementem największym.
Rozważmy zbiór uporządkowany . Łatwo sprawdzić, że jest porządkiem. Wtedy obydwa elementy ( i ) są maksymalne, a żaden z nich nie jest największy, bo są nieporównywalne.
Istnieje też zbiór uporządkowany, w którym istnieje dokładnie jeden element maksymalny, który nie jest elementem największym. Niech będzie elementem takim, że Niech . Zbiór uporządkujemy relacją , gdzie jest naturalną relacją porządku w . Zobacz ilustrację obok- do zbioru liczb naturalnych dodaliśmy jeden element porównywalny tylko z samym sobą. Ponieważ jest porządkiem na , więc łatwo sprawdzić, że jest porządkiem na . Wtedy jest elementem maksymalnym (bo jedyny element, który jest z nim porównywalny to on sam, a więc nie może istnieć żaden większy). W dodatku nie jest elementem największym, bo na przykład nie jest większy od . Nie ma drugiego elementu maksymalnego, gdyż musiałby być liczbą naturalną. Dla każdej liczby naturalnej natomiast istnieje liczba naturalna od niej istotnie większa (czyli liczba naturalna nie może być elementem maksymalnym).
A więc widać, że pojęcia: element maksymalny a element największy, mogą znaczyć co innego. Przyczyną takiego stanu rzeczy, są właśnie elementy nieporównywalne, a dokładniej warunki , a , nie muszą być równoważne, bo elementy mogą być nieporównywalne. Jednak w liniowym zbiorze uporządkowanym (gdzie każde dwa elementy są porównywalne) pojęcia element największy a maksymalny, oraz symetrycznie- element najmniejszy a minimalny się pokrywają. Mówi o tym następny fakt.
Fakt 2. W zbiorze liniowo uporządkowanym element jest maksymalny/minimalny, wtedy i tylko wtedy, gdy jest największy/najmniejszy.
Czyli w zbiorze liniowo uporządkowanym terminy element maksymalny a element największy już znaczą to samo. Symetrycznie dla elementów minimalnych a najmniejszych- w liniowym zbiorze uporządkowanym te pojęcia znaczą to samo.
Dowód:
Gdyby istniał element , który jest największy, ale nie jest maksymalny, to z ostatniego istniałby element silnie większy od . Ale jest elementem największym, zatem jest silnie większy od największego, a tak być nie może. Sprzeczność.
Niech będzie maksymalny. Pokażemy, że jest największy. Ustalmy zatem dowolny element . Przypuśćmy niewprost, że . Ponieważ porządek jest liniowy, więc elementy są porównywalne, i , więc musi być , a skoro tak, to z maksymalności mamy . Ponieważ , to otrzymujemy sprzeczność ze zwrotnością porządku.- Dowód dla elementów najmniejszych, minimalnych jest symetryczny.
Diagramy Hassego
Skończone zbiory uporządkowane wygodnie jest czasem przedstawiać na grafach, tzw. diagramach Hassego. Zobacz ilustrację obok na prawo. Odczytujemy,że w tym zbiorze uporządkowanym Ogólnie, element jest mniejszy od elementu , jeśli element można połączyć drogą z elementem , idąc cały czas w górę( bądź na ukos). Dlatego tutaj
Na diagramie Hassego odczytujemy, że element jest najmniejszy, kiedy wszystkie elementy na tym diagramie dochodzą do niego (w dół). Podobnie odczytujemy element największy (tylko w górę). Zobacz ilustrację obok- tu jest elementem najmniejszym, a jest elementem największym- jest to diagram Hassego dla relacji podzielności na zbiorze
Supremum i infimum
Niech będzie zbiorem uporządkowanym, oraz . Mówimy, że jest ograniczeniem górnym zbioru , gdy dla dowolnego mamy
Czyli ograniczenie górne zbioru , to taki element zbioru , który jest większy lub równy od każdego elementu tego zbioru .
Niech oraz . Mówimy, że jest ograniczeniem dolnym zbioru , gdy dla dowolnego mamy
Podobnie ograniczenie dolne zbioru , to taki element, który jest mniejszy lub równy od każdego elementu tego zbioru .
Niech będzie zbiorem uporządkowanym, . Element nazywamy supremum zbioru , gdy:
1. jest ograniczeniem górnym zbioru . 2. jeśli jest ograniczeniem górnym zbioru , to
Czyli supremum zbioru , to jego ograniczenie górne- najmniejsze z możliwych.
Niech . Element nazywamy infimum zbioru , gdy:
1. jest ograniczeniem dolnym zbioru . 2. jeśli jest ograniczeniem dolnym zbioru , to
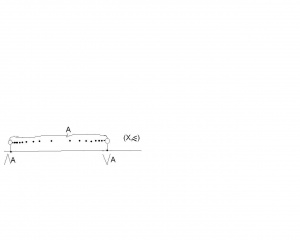
Czyli infimum zbioru to jego ograniczenie dolne- największe z możliwych. Zobacz ilustrację obok.
Łatwo zauważyć, że supremum, o ile istnieje, jest jedyne (bo jest to pewnego rodzaju element najmniejszy). Jeżeli istnieje supremum dla zbioru będziemy je oznaczać .
Tak jak w przypadku supremum, infimum, o ile istnieje, jest jedyne( bo jest to pewnego rodzaju element największy). Jeżeli istnieje infimum dla zbioru , będziemy je oznaczać
Poniżej podaję prosty fakt.
Fakt 3. W zbiorze uporządkowanym , oraz dla zbioru , jeśli element jest elementem największym /najmniejszym, to jest supremum/infimum zbioru .
Czyli element największy zbioru , jest jego supremum. Symetrycznie- element najmniejszy zbioru jest jego infimum.
Dowód:
Niech , przypuśćmy, że element jest elementem największym w. Pokażemy, że jest również supremum . Ponieważ jest elementem największym w , to jest on większy od każdego elementu w tym zbiorze. Zatem jest ograniczeniem górnym dla . Pozostaje pokazać, że to jest najmniejsze ograniczenie górne dla zbioru . Niech będzie ograniczeniem górnym . Jest ono więc większe od każdego elementu . A ponieważ jest elementem największym , to niewątpliwie . Zatem . Z dowolności wyboru ,otrzymujemy, że jest najmniejszym ograniczeniem górnym zbioru , a więc jest supremum zbioru . Dowód dla elementów najmniejszych, infimum jest symetryczny.
Przykład. Dla dowolnego zbioru , jego zbiór potęgowy jest uporządkowany przez inkluzję. Czy dla dowolnej niepustej rodziny istnieje supremum i infimum?
Pokażemy, że dla dowolnej rodziny , mamy oraz (jeśli dodatkowo rodzina jest niepusta), to:
Zauważmy najpierw, że , zatem Pokażemy, że spełnia warunki bycia supremum dla
1. Niech Z własności sumy Wobec dowolności , oznacza to, że jest ograniczeniem górnym rodziny
2. Niech , będzie ograniczeniem górnym rodziny , pod względem inkluzji. Oznacza to, że , dla dowolnego zbioru Zatem każdy zbiór jest podzbiorem , to również jest podzbiorem , czyli . Wobec dowolności , otrzymujemy, że
Niech będzie niepustą rodziną podzbiorów . Pokażemy, że Pokażemy, że spełnia warunki bycia infimum dla
1. Niech Z własności iloczynu , a więc Wobec dowolności , oznacza to, że jest ograniczeniem dolnym rodziny
2. Niech , będzie ograniczeniem dolnym rodziny , pod względem inkluzji. Oznacza to, że , dla dowolnego zbioru Zatem zbiór zawiera się w każdym zbiorze rodziny (niepustej) , to również zawiera się w iloczynie tej rodziny, czyli . Wobec dowolności , otrzymujemy, że
W zbiorze uporządkowanym podzbiór może nie mieć supremum/infimum, i to z różnych przyczyn. Np. rozważmy zbiór uporządkowany przez Wtedy cały zbiór nie ma supremum, bo nie ogranicza z góry , i nie ogranicza z góry . Kolejny przykład będzie dotyczył liniowego porządku. Rozważmy zbiór z naturalnym porządkiem, wtedy cały nie ma supremum, gdyż takie supremum musiałoby być liczbą naturalną będącą ograniczeniem górnym , czyli największą liczbą naturalną, a taka nie istnieje. Wobec czego tutaj nie ma supremum. Tak, zbiory nieograniczone z góry nie mogą mieć supremum, gdyż supremum z definicji jest ograniczeniem górnym. Jednak takie zbiory nieskończone jak mogą mieć supremum, w pewnych zbiorach uporządkowanych( bo mogą być ograniczone z góry), o czym się jeszcze przekonamy. Podobne zależności dostrzegamy dla infimum zbioru.
Łańcuchy i antyłańcuchy
W zbiorze uporządkowanym zbiór nazywamy łańcuchem, gdy każde dwa elementy są porównywalne w sensie rozpatrywanego porządku .
W zbiorze uporządkowanym zbiór nazywamy antyłańcuchem, gdy żadne dwa różne elementy nie są porównywalne. Tzn. dla dowolnych zachodzi:
Ćwiczenie: Czy antyłańcuch może być łańcuchem?
Rozwiązanie: Dla niepustego zbioru uporządkowanego każdy jednoelementowy podzbiór jest antyłańcuchem, jak i łańcuchem.
Na diagramie Hassego łańcuch to zbiór połączonych drogą punktów( tak jak w potocznym łańcuchu)- zobacz ilustrację obok. Antyłańcuch natomiast, to zbiór niepołączonych ze sobą punktów, co przedstawia kolejna ilustracja.
Zachodzi pytanie- czy suma (dwóch) łańcuchów musi być łańcuchem, oraz czy suma antyłańcuchów musi być antyłańcuchem?? Oczywiście suma łańcuchów nie musi być łańcuchem- wystarczy rozważyć dwa łańcuchy stojące obok siebie by się o tym przekonać. Podobnie suma antyłańcuchów nie musi być antyłańcuchem- co przedstawia kolejna ilustracja.
Odnotujmy dwa proste fakty. Dla dowolnego zbioru uporządkowanego każdy jego podzbiór jest również uporządkowany przez , czyli przez relację zawężoną do elementów . Czyli każdy podzbiór zbioru uporządkowanego jest również uporządkowany. Wynika to z faktu, że własności zwrotności, antysymetrii, i przechodniości są spełnione w zbiorze uporządkowanym dla dowolnych elementów , więc będą spełnione również dla dowolnych elementów , jako podzbioru, stąd łatwo sprawdzić, że jest zbiorem uporządkowanym. Kolejny fakt mówi, że dla dowolnego zbioru relacja identyczności na jest relacją porządku. Łatwo sprawdzić, że jest zwrotna i przechodnia. Aby sprawdzić antysymetrię niech oraz . Założenie oznacza, że . W ten zabawnie prosty sposób sprawdziliśmy antysymetrię, więc relacja identyczności jest relacją porządku na zbiorze .
Dla każdego zbioru uporządkowanego , zarówno zbiór jego wszystkich łańcuchów, jak i zbiór jego antyłańcuchów jest uporządkowany przez inkluzję, w myśl twierdzenia 1. Łatwo można pokazać, że zawsze istnieje najmniejszy pod względem inkluzji łańcuch i antyłańcuch- pusty podzbiór . Fakt, że w każdym zbiorze uporządkowanym możemy znaleźć maksymalny łańcuch (podobnie antyłańcuch) jest prawdziwy, przy założeniu aksjomatu wyboru. Będziemy o tym pisać w następnym rozdziale. Natomiast za chwilę opiszemy w prosty sposób kiedy w zbiorze uporządkowanym jest największy łańcuch (i największy antyłańcuch).
Przykład. Rozważmy zbiór uporządkowany relacją podzielności. Wtedy maksymalnymi łańcuchami pod względem inkluzji są:
A maksymalnymi antyłańcuchami są:
W zbiorze uporządkowanym istnieje największy pod względem inkluzji łańcuch dokładnie wtedy, gdy porządek jest liniowy.
Dowód: Jeśli jest zbiorem liniowo uporządkowanym, to łatwo się przekonać, że cały zbiór jest łańcuchem. Ponieważ każdy łańcuch ze swej natury jest podzbiorem , czyli jest mniejszy pod względem inkluzji od , to łańcuch jest największy.
Przypuśćmy nie wprost, że porządek nie jest liniowy. Istnieją wtedy dwa elementy nieporównywalne i . Łatwo się przekonać, że zbiory jednoelementowe , są łańcuchami, zatem są podzbiorami największego łańcucha. Ale wtedy w tym największym łańcuchu znajdują się elementy . Czyli w takim łańcuchu są elementy nieporównywalne i - sprzeczność z definicją łańcucha.
W zbiorze uporządkowanym istnieje największy pod względem inkluzji antyłańcuch dokładnie wtedy, gdy porządek jest relacją identyczności na .
Dowód:
Jeśli , to łatwo się przekonać, że cały zbiór jest antyłańcuchem. Ponieważ każdy antyłańcuch ze swej natury jest podzbiorem , czyli jest mniejszy pod względem inkluzji od , to antyłańcuch jest największy.
Przypuśćmy, że Pokażemy, że nie istnieje wtedy największy antyłańcuch. Przypuśćmy dla dowodu nie wprost, że istnieje i nazywa się . Ponieważ nie jest relacją identyczności na , więc relacja ma w sobie parę , gdzie Oznacza to, ze elementy są porównywalne, i różne. Wtedy łatwo się przekonać, że zbiory jednoelementowe , są antyłańcuchami, zatem są podzbiorami największego antyłańcucha . Ale wtedy w tym największym antyłańcuchu znajdują się elementy . Czyli w takim antyłańcuchu są rózne elementy porównywalne i - sprzeczność z definicją antyłańcucha.
Liniowe porządki
Niech zbiory uporządkowane. Porządek nazywamy rozszerzeniem porządku , gdy dla dowolnych spełniony jest warunek:
Tzn. jeśli jest mniejszy ( lub równy) od względem danego porządku (na ),to tymbardziej musi być mniejsze(lub równe) od względem porządku rozszerzającego. Dla liniowych porządków wygląda to tak, że porządek rozszerzający jest szerszy- zobacz ilustrację obok.
Twierdzenie:
Niech będzie dowolnym ustalonym zbiorem. Niech będzie pewnym zbiorem złożonym z liniowych porządków( samych relacji) określonych na pewnych podzbiorach , takim, że dla dowolnych dwóch liniowych porządków w jeden jest rozszerzeniem drugiego, to wtedy dla relacji , zachodzi i jest liniowym porządkiem na tym zbiorze.
Tzn. suma rodziny liniowych porządków na podzbiorach , i jeśli wiemy, że dla dowolnych dwóch takich liniowych porządków jeden jest rozszerzeniem drugiego, to wtedy suma rodziny takich liniowych porządków jest liniowym porządkiem na swoim polu- zobacz ilustrację obok.
Dowód:
Aby wykazać, że wykażemy inkluzję w obydwie strony.
Aby pokazać, że , to niech . Oznacza to , że przy pewnym . To z kolei zapisujemy a więc dla pewnego liniowego porządku z . Porządek taki jest zwrotny, więc , a więc otrzymujemy, że , lub inaczej , i ponieważ jest prawą współrzędna pary z relacji , to , i
Dowód inkluzji w drugą stronę jest analogiczny. A więc Oznaczmy ten zbiór jako . Wykażemy, że jest liniowym porządkiem na tym zbiorze.
Zwrotność. Niech . Należy pokazać, że , lub inaczej że czyli, że dla pewnego liniowego porządku z . Ale każdy liniowy porządek jest zwrotny, więc powyższy fakt jest prawdziwy. Relacja jest więc zwrotna.
Antysymetria. Niech i . Pokażemy, że . Równoważnie możemy zapisać nasze założenia jako i Pierwszy warunek oznacza, że dla pewnego liniowego porządku z Drugi warunek oznacza, że dla pewnego liniowego porządku z ( niekoniecznie tego samego). Ale wiemy, że dla dowolnych dwóch liniowych porządków z jeden jest rozszerzeniem drugiego, więc jeśli jest rozszerzeniem , to z warunku wynika, że mamy , i ponieważ liniowy porządek jest antysymetryczny, to dostajemy , co należało pokazać. W drugim przypadku jest rozszerzeniem , i wtedy z warunku wynika, że , mamy , i ponieważ liniowy porządek jest antysymetryczny, to dostajemy , co należało pokazać. Antysymetria jest więc pokazana.
Przechodniość. Niech Pokażemy, że Nasze założenia możemy inaczej zapisać jako: oraz Wnioskujemy, że dla pewnego liniowego porządku z , oraz, że dla pewnego liniowego porządku z . Dla porządków , jeden jest rozszerzeniem drugiego, więc jeśli jest rozszerzeniem , to z faktu wynika, że , mamy, że , więc z przechodniości liniowego porządku otrzymujemy, że , a więc , czyli W pozostałym przypadku musi być rozszerzeniem , a wtedy z faktu wynika, że , mamy założenie, że , więc z przechodniości liniowego porządku , dostajemy, że , i również w tym przypadku Relacja jest więc przechodnia.
Dowód spójności jest niestety bardzo żmudny, więc go pomijamy. Wykazaliśmy, że jest porządkiem na swoim polu. Tego twierdzenia użyjemy tylko chyba raz w dowodzie twierdzenia Zermelo. To, że ten porządek jest liniowy nie będzie nam wtedy konieczne.