Funkcje

W tym rozdziale wprowadzamy pojęcie funkcji. W teorii zbiorów funkcje, są relacjami, które spełniają dodatkowy warunek jednoznaczności. A więc funkcja jako relacja jest zbiorem, którego elementami są pary uporządkowane.

Relację [math]f\subset X \times Y[/math] nazywamy funkcją ze zbioru [math]X[/math] w zbiór [math]Y[/math], jeśli ma poniższe własności:

[math]1. \ \left( x,y_{1}\right) \in f \wedge \left( x,y_{2}\right) \in f \Longrightarrow y_{1}=y_{2}. \\ 2. \ f_L = X.[/math]

Ilustracja funkcji

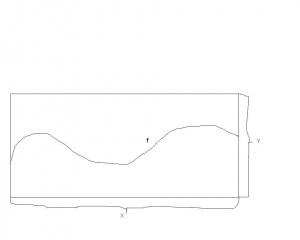
Czyli funkcja [math]f\subset X \times Y[/math] to relacja taka, że do każdego elementu [math]x[/math] ze zbioru [math]X[/math] można dobrać dokładnie jeden element [math]y\in Y[/math] będący z nim w relacji [math]f[/math]. Zobacz (uproszczoną) ilustrację obok- na przecięciu z każdym odcinkiem pionowym mamy dokładnie jeden element [math]y\in Y[/math]. Oczywiście rysunek jest uproszczony- wykres może być bardziej skomplikowany.

Dla zainteresowanych mogę dokładniej wyjaśnić definicję. Pierwsza własność mówi dokładnie tyle, że jeśli do jakiegoś elementu [math]x[/math], możemy dobrać elementy [math]y_{1}[/math] i [math]y{_2}[/math] tak, aby obydwa były w relacji z [math]x[/math], to muszą one być sobie równe, a więc do każdego elementu zbioru [math]X[/math] można dobrać co najwyżej jeden element, będący z nim w relacji [math]f[/math]. Druga własność mówi, że każdy element [math]x\in X[/math] należy do [math]f_{L}[/math], a więc do każdego elementu ze zbioru [math]X[/math] da się dobrać przynajmniej jeden element [math]y\in Y[/math], będący z nim w relacji [math]f[/math]. Łącznie te dwa wnioski oznaczają, że do każdego elementu [math]x[/math] ze zbioru [math]X[/math] można dobrać dokładnie jeden element [math]y\in Y[/math], będący z nim w relacji [math]f[/math]. Często będziemy używać skrótowego zapisu [math]f:X \rightarrow Y[/math], który będzie oznaczał, że [math]f[/math] jest funkcją ze zbioru [math]X[/math] w zbiór [math]Y.[/math] Mówimy, że funkcja [math]f[/math] przekształca zbiór [math]X[/math] w zbiór [math]Y[/math]. Zbiór wszystkich funkcji ze zbioru [math]X[/math] w zbiór [math]Y[/math], oznaczamy jako [math]Y^X[/math]. Zbiór ten definiujemy jako:

[math]Y^{X}=\left\{ f\in P\left( X\times Y\right) \ \ \left( f\subset X\times Y\right) \Bigl| \ \ f \hbox{ jest funkcją ze zbioru } X \hbox{ w zbiór } Y\right\}.[/math]

Przykłady : [math]X=Y=\left\{ 0,1,2\right\} [/math] relacja [math] f=\left\{ \left( 0,0\right),\left( 1,0\right),\left( 2,1\right) \right\} [/math] jest funkcją, ale już relacja [math]g=\left\{ \left( 0,0\right),\left( 0,1\right) \right\}[/math] funkcją nie jest, bo zerze przyporządkowuje dwie wartości- [math]0[/math] i [math]1[/math].

[math]X[/math]-dowolny zbiór, [math]Y=\left\{ 0,1\right\}. [/math] Relacja [math]X\times\left\{ 0\right\}[/math] jest funkcją, ale nie jest już funkcją relacja [math]X\times\left\{ 0,1\right\}[/math] jeśli tylko zbiór [math]X[/math] jest niepusty. Wystarczy bowiem wyciągnąć z niepustego zbioru [math]X[/math] element pewien [math]x\in X[/math], i utworzyć pary [math]\left( x,0\right) ,\left( x,1\right) [/math], co pokazuje, że elementowi [math]x[/math] przypisaliśmy dwie wartości, a więc nie jest to funkcja.

Dla dowolnego zbioru [math]X[/math] relacja [math]I_X[/math] identyczności na [math]X[/math] jest funkcją ze zbioru [math]X[/math] w ten sam zbiór [math]X[/math]. Aby to wykazać, to przypuśćmy, że [math]\left( x,x _{1} \right)\in I_X[/math] i [math]\left( x,x _{2} \right)\in I_X[/math]. Założenie [math]\left( x,x _{1} \right)\in I_X[/math] oznacza, że [math]x=x_1[/math], podobnie założenie [math]\left( x,x _{2} \right)\in I_X[/math] oznacza, że [math]x=x_2[/math]; zatem [math]x_1=x_2[/math]. Łatwo się też przekonać, że zgodnie z intuicją [math]\left( I_{X}\right) _{L}=X [/math]. Zatem [math]I_X[/math] jest funkcją z [math]X[/math] w [math]X[/math].

Dla funkcji wprowadzimy podstawowe oznaczenia. Rozważmy funkcję [math]f:X \rightarrow Y[/math]. Zbiór [math]X[/math] nazywamy dziedziną funkcji [math]f[/math], a zbiór [math]Y[/math] nazywamy przeciwdziedziną funkcji [math]f[/math]. Dla dowolnego [math]x\in X[/math], jedyny element [math]y[/math], dla którego [math](x,y)\in f[/math], to oznaczamy go przez [math]f(x)[/math], podobnie fakt [math](x,y)\in f[/math] notujemy jako [math]f(x)=y.[/math] Mówimy wtedy, że funkcja [math]f[/math] przyporządkowuje elementowi [math]x[/math] element [math]y[/math]. Elementy [math]X[/math] nazywamy argumentami funkcji [math]f[/math]. Zbiór [math]f_P[/math] nazywamy zbiorem wartości funkcji [math]f[/math], a jego elementy wartościami funkcji [math]f[/math].

Funkcja różnowartościowa i 'na'

Funkcję [math]f:X \rightarrow Y[/math]nazywamy różnowartościową, jeśli różnym argumentom przypisuje różne wartości, tzn. dla dowolnych [math]x,y \in X[/math], zachodzi:

[math]x \neq y \Longrightarrow f\left( x\right) \neq f\left( y\right) .[/math]

Lub równoważnie

[math]f\left( x\right)=f\left( y\right) \Longrightarrow x=y.[/math]

Powyższy warunek mówi, że jeśli funkcja argumentom [math]x,y[/math] przypisuje tą samą wartość, to te argumenty muszą być równe.

Przykłady: Funkcja [math]f:\left\{ 0,1\right\} \rightarrow \left\{ 0,1\right\},[/math] dana jako: [math]f=\left\{ \left( 0,1\right) , \left( 1,0\right)\right\}[/math] jest różnowartościowa. Kolejny przykład: funkcja, która każdej liczbie naturalnej przypisuję liczbę naturalną dwukrotnie większą jest różnowartościowa. Funkcja [math]f:\left\{ 0,1\right\} \rightarrow \left\{ 0,1\right\}[/math], dana jako: [math]f=\left\{ \left( 0,0\right) , \left( 1,0\right)\right\}[/math] nie jest różnowartościowa. Podobnie [math]f:\left\{ \emptyset, \left\{ \emptyset\right\} \right\} \rightarrow \left\{ \emptyset\right\}[/math] dana jako: [math]f=\left\{ \left( \emptyset,\emptyset\right) ,\left( \left\{ \emptyset\right\} ,\emptyset\right) \right\}[/math] nie jest różnowartościowa, bo elementom [math]\emptyset, \left\{ \emptyset\right\}[/math] przypisuję tą samą wartość- [math]\emptyset[/math].Funkcja [math]f:\mathbb{R} \rightarrow \mathbb{R}[/math] dana jako: [math]f\left( x\right)=x ^{2}[/math] nie jest różnowartościowa, bo [math]f\left( 1\right) =f\left( -1\right) .[/math]

Funkcję [math]f:X \rightarrow Y[/math] nazywamy 'na' zbiór [math]Y[/math], gdy [math]f_P=Y[/math], tzn. gdy każdy element [math]y[/math] ze zbioru [math]Y[/math] jest wartością funkcji na jakimś argumencie ze zbioru [math]X[/math], czyli istnieje [math]x\in X[/math] takie, że [math]y=f(x).[/math]

A więc funkcja [math]f:X \rightarrow Y[/math] jest 'na' zbiór [math]Y[/math], gdy jej zbiór wartości jest całą przeciwdziedziną [math]Y.[/math]

Przykłady: funkcja [math]f:\mathbb{N} \rightarrow \mathbb{N}[/math], dana jako [math]f(n)=n+1[/math] nie jest 'na' [math]\mathbb{N}[/math]. Funkcja [math]f:\mathbb{R} \rightarrow \mathbb{R}_+\cup\{ 0\}[/math], dana jako [math]f(x)=x^2[/math] jest 'na'. Kolejny przykład: Niech [math]a[/math] będzie ustalonym elementem. Funkcja [math]f:\mathbb{N} \rightarrow \{ a\} [/math] dana jako; [math]f(n)=a[/math] jest 'na'- jest stale równa [math]a.[/math]

Ilustracja bijekcji

Funkcję [math]f:X \rightarrow Y[/math] nazywamy bijekcją (lub wzajemnie jednoznaczną), gdy [math]f[/math] jest różnowartościowa i 'na' zbiór [math]Y.[/math]

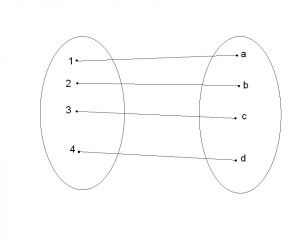
Każda bijekcja pomiędzy dwoma zbiorami, dobiera elementy tych zbiorów w pary- zobacz ilustrację obok.

Obrazy i przeciwobrazy

Obraz zbioru przez funkcję

Dla dowolnych zbiorów [math]X,Y[/math] oraz dowolnej funkcji [math]f:X\rightarrow Y[/math], i dla dowolnego zbioru [math]A\subset X[/math] definiujemy zbiór:

[math]\stackrel{ \rightarrow }{f}\left( A\right)=\left\{ f(x)\Bigl| \ \ x\in A\right\}= \{y\in Y: \bigvee_{x\in A} f(x)=y\}=\left\{ f(x)\Bigl| \ \ x\in A\right\} .[/math]

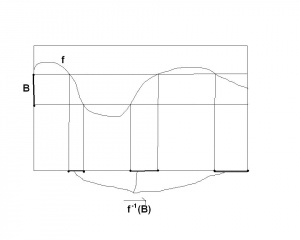
Dla dowolnego zbioru [math]A\subset X[/math] zbiór [math]\stackrel{ \rightarrow }{f}\left( A\right)[/math] nazywamy obrazem zbioru [math]A[/math] przez funkcję [math]f[/math]. Jest to zbiór wartości funkcji [math]f[/math] liczonych dla argumentów ze zbioru [math]A[/math]. Zobacz ilustrację obok.

Przykład: Niech [math]f:\mathbb{N} \rightarrow \mathbb{N}[/math] będzie dana jako: [math]f\left( n\right)=2n.[/math] Wtedy: [math]\stackrel{ \rightarrow }{f}\left( \mathbb{N}\right)[/math] jest zbiorem liczb parzystych, [math]\stackrel{ \rightarrow }{f}\left( \left\{ 1,2\right\} \right)=\left\{ 2,4\right\}[/math], obrazem zbioru liczb parzystych przez funkcję [math]f[/math] jest zbiór liczb naturalnych podzielnych przez [math]4[/math].

Przeciwobraz zbioru przez funkcję

W podobny sposób definiujemy przeciwobrazy zbiorów przez funkcję. Dla dowolnej funkcji [math]f:X\rightarrow Y[/math] przeciwobrazem zbioru [math]B \subset Y[/math] przez funkcję [math]f[/math] nazwiemy zbiór tych elementów zbioru [math]X[/math], którym funkcja przypisuje wartości ze zbioru [math]B[/math]. Czyli dla dowolnego zbioru [math]B \subset Y[/math] definiujemy zbiór:

[math]\stackrel{ \rightarrow }{f ^{-1} }\left( B\right)=\left\{ x\in X\Bigl| \ \ f\left( x\right) \in B\right\}.[/math]

który to zbiór nazywamy przeciwobrazem zbioru [math]B[/math] przez funkcję [math]f[/math]. Jest to zbiór tych argumentów, którym funkcja przypisuję wartości ze zbioru [math]B[/math]. Zobacz ilustrację obok.

Przykład: Niech [math]f:\mathbb{N} \rightarrow \mathbb{N}[/math] będzie dana jako: [math]f\left( n\right)=2n.[/math] Wtedy: [math]\stackrel{ \rightarrow }{f ^{-1} }\left( \left\{ 1,2\right\} \right)=\left\{ 1\right\}[/math], przeciwobrazem zbioru liczb nieparzystych przez funkcję [math]f[/math] jest zbiór pusty, przeciwobrazem zbioru liczb naturalnych podzielnych przez [math]4[/math], przez funkcję [math]f[/math], jest zbiór liczb parzystych.

Poniżej podaję prosty fakt.

Dla dowolnej funkcji [math]f:X \rightarrow Y[/math], oraz zbiorów [math]A,B\subset X[/math], zachodzi:

[math]A\subset B \rightarrow \stackrel{ \rightarrow }{f}\left( A\right) \subset \stackrel{ \rightarrow }{f}\left( B\right).[/math]

Czyli jeśli na podzbiorach dziedziny [math]X[/math] zachodzi inkluzja, to taka sama (zgodna) inkluzja występuje na odpowiadającym im obrazach.

Prosty dowód:

Załóżmy, że [math]A\subset B[/math]. Pokazujemy, że [math]\stackrel{ \rightarrow }{f}\left( A\right) \subset \stackrel{ \rightarrow }{f}\left( B\right).[/math] Niech [math]y\in\stackrel{ \rightarrow }{f}\left( A\right).[/math] Oznacza to, że [math]y=f(x)[/math], przy pewnym [math]x\in A[/math]. Ponieważ mamy założenie, że [math]A\subset B[/math], to [math]x\in B[/math], zatem [math]y=f(x)[/math] przy [math]x\in B[/math], a zatem [math]y\in \stackrel{ \rightarrow }{f}\left( B\right)[/math], i [math]\stackrel{ \rightarrow }{f}\left( A\right) \subset \stackrel{ \rightarrow }{f}\left( B\right).\square[/math]

Kolejny podstawowy fakt:

Dla dowolnej funkcji [math]f:X \rightarrow Y[/math], oraz zbiorów [math]A,B\subset X[/math], mamy:

[math]\stackrel{ \rightarrow }{f}\left( A \cup B\right) = \stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right) .[/math]

Czyli obraz sumy dwóch podzbiorów dziedziny, taki obraz sumy jest równy sumie obrazów tych zbiorów.

Dowód:

Z poprzedniego faktu, który mówi, że branie obrazu jest zgodne z zawieraniem( inkluzją), otrzymujemy, że [math]\stackrel{ \rightarrow }{f}\left( A\right) \subset \stackrel{ \rightarrow }{f}\left( A\cup B\right).[/math] oraz, że [math]\stackrel{ \rightarrow }{f}\left( B\right) \subset \stackrel{ \rightarrow }{f}\left( A \cup B\right).[/math] Zatem zbiory [math]\stackrel{ \rightarrow }{f}\left( A\right) ,\stackrel{ \rightarrow }{f}\left( B\right)[/math] są podzbiorami zbioru [math]\stackrel{ \rightarrow }{f}\left( A\cup B\right)[/math], więc również ich suma jest podzbiorem tego zbioru, czyli [math]\stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right) \subset \stackrel{ \rightarrow }{f}\left( A \cup B\right).[/math] Aby pokazać inkluzję w drugą stronę, to niech [math]y\in\stackrel{ \rightarrow }{f}\left( A \cup B\right)[/math]. Oznacza to, że [math]y=f(x)[/math], przy pewnym [math]x\in A \cup B[/math]. Jeśli [math]x\in A[/math], to [math]y=f(x)[/math] przy [math]x\in A[/math], zatem [math]y\in\stackrel{ \rightarrow }{f}\left( A\right)[/math], a jeśli [math]x\in B,[/math] to [math]y=f(x)[/math] przy [math]x\in B[/math], zatem [math]y\in\stackrel{ \rightarrow }{f}\left( B\right)[/math], zatem w obydwu przypadkach [math]y\in \stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right),[/math] i [math]\stackrel{ \rightarrow }{f}\left( A \cup B\right) \subset \stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right)[/math], a więc [math]\stackrel{ \rightarrow }{f}\left( A \cup B\right) = \stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right). \square[/math]

Jeszcze jeden prosty fakt:

Dla dowolnej funkcji [math]f:X \rightarrow Y[/math], mamy:[math]\stackrel{ \rightarrow }{f}\left( \left\{ \right\} \right)=\left\{ \right\} .[/math]

Dowód: Gdyby [math]\stackrel{ \rightarrow }{f}\left( \left\{ \right\} \right) \neq \left\{ \right\}[/math], to istniałby element [math]y\in\stackrel{ \rightarrow }{f}\left( \left\{ \right\} \right)[/math], a więc [math]y=f(x),[/math] przy [math]x\in\left\{ \right\}[/math], a więc [math]x\in\left\{ \right\}[/math]-sprzeczność. [math]\square[/math]

Dla dowolnej funkcji [math]f:X \rightarrow Y[/math], przeciwobrazy różnych zbiorów jednoelementowych są rozłączne. Aby się o tym przekonać, niech [math]y _{1},y _{2}\in Y,[/math] będą różnymi elementami zbioru [math]Y[/math]. Chcemy sprawdzić, że zbiory [math]\stackrel{ \rightarrow }{f ^{-1} }\left\{ y _{1} \right\}[/math] oraz [math]\stackrel{ \rightarrow }{f ^{-1} }\left\{ y _{2} \right\} [/math] są rozłączne, czyli nie mają wspólnych elementów. Gdyby miały wspólny element [math]x\in X[/math], to wtedy z definicji przeciwobrazu [math]f\left( x\right) \in \left\{ y _{1} \right\}[/math] oraz [math]f\left( x\right) \in \left\{ y _{2} \right\}[/math], czyli [math]f(x)=y _{1}[/math] oraz [math]f(x)=y _{2}[/math], co wobec różności elementów [math]y_1,y_2[/math] daję sprzeczność z definicją funkcji.

Złożenie funkcji

Ilustracja złożenia funkcji

Niech [math]X,Y,Z[/math] będą zbiorami, a [math]f:X \rightarrow \textbf{Y}[/math] oraz [math]g:\textbf{Y} \rightarrow Z[/math] dowolnymi funkcjami. Złożeniem funkcji [math]f[/math] i [math]g[/math] nazywamy funkcję [math]g\circ f[/math] ( uwaga!- jest odwrócona kolejność) [math]g\circ f:X \rightarrow Z[/math] określoną jako:

[math]\left( g\circ f\right)\left( x\right)=g\left( f\left( x\right) \right),\hbox{ dla dowolnego } x\in X.[/math]

Przykład: Niech [math]f:\mathbb{N} \rightarrow \mathbb{N}[/math] będzie dana jako:[math]f\left( n\right) =n+1[/math], a [math]g:\mathbb{N} \rightarrow P\left( \mathbb{N}\right)[/math] będzie dana jako [math]g\left( n\right) =\left\{ n\right\}.[/math] Wtedy [math]g\circ f:\mathbb{N} \rightarrow P\left( \mathbb{N}\right)[/math] działa tak:

[math]\left( g\circ f\right)\left( n\right)=g\left( f\left( n\right) \right)=\left\{ n+1\right\}, \hbox{ dla dowolnej liczby naturalnej } n.[/math]

Złożenie funkcji nie musi być przemienne. Na przykład niech [math]f:\mathbb{N} \rightarrow \mathbb{N}[/math] będzie dana jako:[math]f\left( n\right) =n+1[/math], a [math]g:\mathbb{N} \rightarrow \mathbb{N}[/math] będzie dana jako [math]g\left( n\right) = 2n.[/math] Wtedy [math]g\circ f:\mathbb{N} \rightarrow \mathbb{N}[/math] działa tak:

[math]\left( g\circ f\right)\left( n\right)=g\left( f\left( n\right) \right)=g\left( n+1\right)=2\left( n+1\right)=2n+2.[/math] Natomiast [math]f\circ g:\mathbb{N} \rightarrow \mathbb{N}[/math] działa tak:

[math]\left( f\circ g\right)\left( n\right)=f\left( g\left( n\right) \right)=f\left( 2n\right)=2n+1 \neq 2n+2[/math], zatem [math]g\circ f \neq f\circ g[/math]: