Funkcje

W tym rozdziale wprowadzamy pojęcie funkcji. W teorii zbiorów funkcje, są relacjami, które spełniają dodatkowy warunek jednoznaczności. A więc funkcja jako relacja jest zbiorem, którego elementami są pary uporządkowane.

Relację [math]f\subset X \times Y[/math] nazywamy funkcją ze zbioru [math]X[/math] w zbiór [math]Y[/math], jeśli ma poniższe własności:

[math]1. \ \left( x,y_{1}\right) \in f \wedge \left( x,y_{2}\right) \in f \Longrightarrow y_{1}=y_{2}. \\ 2. \ f_L = X.[/math]

Ilustracja funkcji

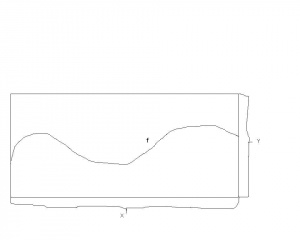
Czyli funkcja [math]f\subset X \times Y[/math] to relacja taka, że do każdego elementu [math]x[/math] ze zbioru [math]X[/math] można dobrać dokładnie jeden element [math]y\in Y[/math] będący z nim w relacji [math]f[/math]. Zobacz (uproszczoną) ilustrację obok- na przecięciu z każdym odcinkiem pionowym mamy dokładnie jeden element [math]y\in Y[/math]. Oczywiście rysunek jest uproszczony- wykres może być bardziej skomplikowany.

Dla zainteresowanych mogę dokładniej wyjaśnić definicję. Pierwsza własność mówi dokładnie tyle, że jeśli do jakiegoś elementu [math]x[/math], możemy dobrać elementy [math]y_{1}[/math] i [math]y{_2}[/math] tak, aby obydwa były w relacji z [math]x[/math], to muszą one być sobie równe, a więc do każdego elementu zbioru [math]X[/math] można dobrać co najwyżej jeden element, będący z nim w relacji [math]f[/math]. Druga własność mówi, że każdy element [math]x\in X[/math] należy do [math]f_{L}[/math], a więc do każdego elementu ze zbioru [math]X[/math] da się dobrać przynajmniej jeden element [math]y\in Y[/math], będący z nim w relacji [math]f[/math]. Łącznie te dwa wnioski oznaczają, że do każdego elementu [math]x[/math] ze zbioru [math]X[/math] można dobrać dokładnie jeden element [math]y\in Y[/math], będący z nim w relacji [math]f[/math]. Często będziemy używać skrótowego zapisu [math]f:X \rightarrow Y[/math], który będzie oznaczał, że [math]f[/math] jest funkcją ze zbioru [math]X[/math] w zbiór [math]Y.[/math] Mówimy, że funkcja [math]f[/math] przekształca zbiór [math]X[/math] w zbiór [math]Y[/math]. Zbiór wszystkich funkcji ze zbioru [math]X[/math] w zbiór [math]Y[/math], oznaczamy jako [math]Y^X[/math]. Zbiór ten definiujemy jako:

[math]Y^{X}=\left\{ f\in P\left( X\times Y\right) \ \ \left( f\subset X\times Y\right) \Bigl| \ \ f \hbox{ jest funkcją ze zbioru } X \hbox{ w zbiór } Y\right\}.[/math]

Przykłady : [math]X=Y=\left\{ 0,1,2\right\} [/math] relacja [math] f=\left\{ \left( 0,0\right),\left( 1,0\right),\left( 2,1\right) \right\} [/math] jest funkcją, ale już relacja [math]g=\left\{ \left( 0,0\right),\left( 0,1\right) \right\}[/math] funkcją nie jest, bo zerze przyporządkowuje dwie wartości- [math]0[/math] i [math]1[/math].

[math]X[/math]-dowolny zbiór, [math]Y=\left\{ 0,1\right\}. [/math] Relacja [math]X\times\left\{ 0\right\}[/math] jest funkcją, ale nie jest już funkcją relacja [math]X\times\left\{ 0,1\right\}[/math] jeśli tylko zbiór [math]X[/math] jest niepusty. Wystarczy bowiem wyciągnąć z niepustego zbioru [math]X[/math] element pewien [math]x\in X[/math], i utworzyć pary [math]\left( x,0\right) ,\left( x,1\right) [/math], co pokazuje, że elementowi [math]x[/math] przypisaliśmy dwie wartości, a więc nie jest to funkcja.

Dla funkcji wprowadzimy podstawowe oznaczenia. Rozważmy funkcję [math]f:X \rightarrow Y[/math]. Zbiór [math]X[/math] nazywamy dziedziną funkcji [math]f[/math], a zbiór [math]Y[/math] nazywamy przeciwdziedziną funkcji [math]f[/math]. Dla dowolnego [math]x\in X[/math], jedyny element [math]y[/math], dla którego [math](x,y)\in f[/math], to oznaczamy go przez [math]f(x)[/math], podobnie fakt [math](x,y)\in f[/math] notujemy jako [math]f(x)=y.[/math] Mówimy wtedy, że funkcja [math]f[/math] przyporządkowuje elementowi [math]x[/math] element [math]y[/math]. Elementy [math]X[/math] nazywamy argumentami funkcji [math]f[/math]. Zbiór [math]f_P[/math] nazywamy zbiorem wartości funkcji [math]f[/math], a jego elementy wartościami funkcji [math]f[/math].