Relacje: Różnice pomiędzy wersjami
(→Relacje) |
(→Relacje) |
||
| Linia 147: | Linia 147: | ||
Ilustracja tych operacji jest podobna do ilustracji działań mnogościowych na zbiorach- zobacz ilustrację obok. Różnica polega na tym, że mamy wprowadzoną strukturę iloczynu kartezjańskiego, i na punkty patrzymy nie na jako zwykłe elementy, tylko jak na pary uporządkowane. | Ilustracja tych operacji jest podobna do ilustracji działań mnogościowych na zbiorach- zobacz ilustrację obok. Różnica polega na tym, że mamy wprowadzoną strukturę iloczynu kartezjańskiego, i na punkty patrzymy nie na jako zwykłe elementy, tylko jak na pary uporządkowane. | ||
| + | |||
| + | Co więcej, niech <math>\mathbb{A}</math> będzie pewną rodziną relacji z <math>X</math> do <math>Y</math>. Wtedy <math>\bigcup \mathbb{A}</math>- suma rodziny relacji z <math>X</math> do <math>Y</math>, a więc suma rodziny podzbiorów <math>X\times Y</math> jest podzbiorem <math>X\times Y</math>, a więc jest relacją z <math>X</math> do <math>Y</math>. Stąd mamy ważne: | ||
| + | |||
| + | '''Twierdzenie 2.1.''' ''Suma dowolnej rodziny relacji z <math>X</math> do <math>Y</math> jest relacją z <math>X</math> do <math>Y</math>. '' | ||
| + | |||
| + | Dla takiej relacji, mamy: <math>\left( x,y\right) \in \bigcup \mathbb{A}\Longleftrightarrow \left( x,y\right) \in R</math>, dla pewnej relacji <math>R\in\mathbb{A}.</math> | ||
| + | |||
| + | Tzn. dwa elementy są ze sobą w relacji <math>\bigcup \mathbb{A}</math>, gdy są z sobą w relacji <math>R</math>, dla pewnej relacji <math>R</math> z rodziny relacji <math>\mathbb{A}.</math> | ||
| + | |||
| + | Podobnie możemy określić iloczyn rodziny relacji. Dla niepustej rodziny <math>\mathbb{A}</math> relacji z <math>X</math> do <math>Y</math>, relacja <math>\bigcap \mathbb{A}</math>, to taka relacja, że dwa elementy są ze sobą w relacji <math>\bigcap \mathbb{A}</math>, gdy są z sobą w relacji <math>R</math>, dla każdej relacji <math>R\in\mathbb{A}.</math> | ||
Wersja z 02:37, 9 maj 2018
Niech będą dowolnymi elementami (zbiorami). Przez parę uporządkowaną rozumiemy zbiór
Uwaga:
Parę uporządkowaną można też zdefiniować w inny sposób. Chodzi jednak o to, by dla takich par spełniona była własność zapowiedziana w pierwszym rozdziale, która mówi, że jeśli jedna para uporządkowana różni się od drugiej pary, choć na pierwszej czy choć na drugiej współrzędnej, to te pary uporządkowane są różne. A więc pokażemy, że przy naszej definicji pary uporządkowanej, zachodzi:
Twierdzenie 1. Dla dowolnych , mamy:
Oczywiście pierwsza równoważność to tylko zastosowanie definicji, interesuje nas druga równoważność, a w zasadzie implikacja .
Dowód: Załóżmy zatem, że
Mamy , więc , a więc lub . W pierwszym przypadku , ale w drugim również jest tak, mamy bowiem, z zasady równości zbiorów , że , a więc . Wiemy już, ze pierwsze współrzędne równych par są równe:
Dalej przeprowadzimy dowód przez rozważenie przypadków.
Jeżeli , to , zatem , więc ponieważ , to z zasady równości zbiorów , a więc , i dalej podobnie , czyli , co należało pokazać.
W przeciwnym przypadku, gdy , to wtedy . Ponieważ , więc . Daje to dwie możliwości: albo , co prowadzi do -sprzeczność. Musi więc zajść drugi przypadek , co daje , i ponieważ to , co należało pokazać.
Dowód jest oczywisty, teza wynika wprost z założeń i zasady równości zbiorów.
Ćwiczenie 2. Dla każdej pary uporządkowanej , udowodnij, że
To ćwiczenie ma bardziej charakter formalny. Przypomnijmy bowiem, że jedynymi przez nas rozważanymi obiektami (bytami) są zbiory. Wobec czego para uporządkowana jest zbiorem ( patrz definicja na początku tego rozdziału), jest to zbiór złożony ze zbiorów, bo elementy zbiorów są również zbiorami, więc możemy utworzyć iloczyn rodziny , otrzymując zbiór - znowu zbiór złożony ze zbiorów, i wtedy iloczyn takiej rodziny zbiorów , gdzie ma być równe zbiorowi ( współrzędne par uporządkowanych są również zbiorami).
Rozwiązanie:
Zatem
Pojęcie pary uporządkowanej jest potrzebne do wprowadzenia iloczynu kartezjańskiego, a potem relacji.
Iloczyn kartezjański
Iloczynem kartezjańskim zbiorów , to zbiór
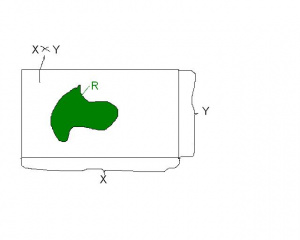
Czyli jest to zbiór wszystkich par uporządkowanych elementów kolejnych zbiorów . Np. Graficzną ilustracją iloczynu kartezjańskiego jest prostokąt- zobacz ilustracje obok. Na ogół - aby się o tym przekonać wyznacz np. i
Podstawowe własności iloczynu kartezjańskiego:
Twierdzenie 1.1. Dla dowolnych zbiorów :
Dowód:
1. Nie wprost. Gdyby iloczyn kartezjański byłby niepusty, to istniałaby para , a więc wtedy i , a zbiór pusty nie posiada elementów, a świadczy o tym, że posiada- sprzeczność. Dowód drugiej równości jest analogiczny.
Nim przejdziemy do dalszych dowodów. potrzebny będzie nam następujący prosty fakt: dla dowolnych oraz dowolnych zbiorów , mamy:
Wynika to z definicji iloczynu kartezjańskiego. Jedyne, co wymaga krótkiego uzasadnienia, to wynikanie
Jeżeli , to , gdzie . Wtedy jednak z twierdzenia 1, mamy i , czyli i .
Przechodzimy do dowodu punktu 2.
Ponieważ obydwa zbiory są zbiorami par uporządkowanych, więc wykażemy, że dowolna para należy do jednego zbioru wtedy i tylko wtedy, gdy należy do drugiego. Weźmy dowolną parę , wtedy na podstawie wprowadzonej własności i definicji sumy dwóch zbiorów:
Zatem, (patrz komentarz początek) Dowód drugiej równości jest analogiczny.
3. Ponieważ obydwa zbiory są zbiorami par uporządkowanych, więc znowu wykażemy, że dowolna para należy do jednego zbioru wtedy i tylko wtedy, gdy należy do drugiego. Weźmy dowolną parę , wtedy:
co należało otrzymać.
4. Na tej samej zasadzie co poprzednio, weźmy dowolną parę . Wtedy:
co należało otrzymać. Dowód jest zakończony.
Fakt 1.2. Dla dowolnych zbiorów , mamy:
Czyli jeden iloczyn kartezjański będzie się zawierać w drugim iloczynie kartezjańskim , jeśli tylko ten mniejszy (pod względem inkluzji) iloczyn kartezjański ma mniejsze odpowiednie składowe- czyli gdy zbiór mniejszy jest od , i mniejszy jest od - to wtedy iloczyn kartezjański mniejszych zbiorów jest mniejszy od odpowiedniego mu iloczynu kartezjańskiego większych zbiorów (mniejszy,większy należy rozumieć jako słabo mniejszy,słabo większy- dopuszczamy równość zbiorów).
Dowód: Zakładamy, że i , chcemy pokazać, że Niech Zatem należy do zbioru , należy do . Ponieważ z założenia , to należy do . Podobnie, ponieważ , to należy do . Z tych dwóch ostatnich wniosków otrzymujemy, że Zatem
Szczególnym przypadkiem powyższego twierdzenia, jest fakt, że dla dowolnych zbiorów , mamy:
Aby to udowodnić, weźmy dowolne zbiory , takie, że . Stosujemy ten Fakt 1.2. do tych samych zbiorów, i zbioru . Ponieważ mamy, że , i , to stosując ten fakt dostajemy, że
Podobnie szczególnym przypadkiem tego Faktu 1.2., jest fakt, że dla dowolnych zbiorów , mamy:
Dokładana konstrukcja iloczynu kartezjańskiego została omówiona w dodatku dla dociekliwych Dla dociekliwych, gdzie została przedstawiona konstrukcja zgodna z aksjomatem wycinania.
Nim przejdziemy dalej do tematu relacji odnotujmy jeszcze zapomniane dwa proste fakty. Pierwszy mówi, że dla dowolnych zbiorów mamy:
Czyli, że suma większych zbiorów (pod względem inkluzji) jest większa. Prosty dowód (trzeba tylko rozważyć dwa przypadki ze względu na przynależność do sumy) pozostawiamy czytelnikowi.
Drugi prosty fakt jest podobny- dotyczy tylko iloczynu. Dla dowolnych zbiorów mamy:
Czyli iloczyn większych zbiorów jest większy. Dowód czytelnikowi nie nastręczy trudności.
Relacje
Podstawowym pojęciem (i fundamentalnym) teorii mnogości jest pojęcie relacji.
Niech będą zbiorami. Relacją między zbiorami a , nazywamy każdy podzbiórCzyli tworzymy najpierw iloczyn kartezjański , każdy podzbiór tego zbioru to przykład relacji między a . Zobacz ilustrację obok.
Ważne relacje:
relacja pusta( zbiór pusty jest podzbiorem każdego zbioru).
- relacja pełna (każdy zbiór jest podzbiorem swoim własnym, więc również spełnia to iloczyn ).
Relacją w zbiorze , nazywamy każdy podzbiór
Przykładem znowu może być relacja pusta, relacja totalna , ale również:
Relacja identyczności- dwa elementy są w relacji gdy są identyczne, równe.
Gdy , gdzie , to mówimy, że elementy są ze sobą w relacji . Zapisujemy to też jako: . Też dla innych oznaczeń relacji- jeśli oznaczymy relację przez np. , to fakt, że elementy są ze sobą w relacji , zapiszemy jako: .
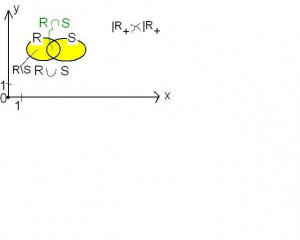
Na relacjach można wykonywać działania mnogościowe. I tak, dla relacji relacja , to taka relacja, że dwa elementy są ze sobą w relacji , jeśli tylko są ze sobą w relacji , oraz wtedy, jeśli tylko są ze sobą w relacji . Czyli .
Podobnie, dla relacji relacja , to taka relacja, że dwa elementy są ze sobą w relacji , jeśli są ze sobą w relacji , oraz równocześnie są ze sobą w relacji . Czyli
Podobnie, różnica relacji - relacja , to taka relacja, że dwa elementy są ze sobą w relacji , gdy są ze sobą w relacji i nie są ze sobą w relacji , tzn.
Ilustracja tych operacji jest podobna do ilustracji działań mnogościowych na zbiorach- zobacz ilustrację obok. Różnica polega na tym, że mamy wprowadzoną strukturę iloczynu kartezjańskiego, i na punkty patrzymy nie na jako zwykłe elementy, tylko jak na pary uporządkowane.
Co więcej, niech będzie pewną rodziną relacji z do . Wtedy - suma rodziny relacji z do , a więc suma rodziny podzbiorów jest podzbiorem , a więc jest relacją z do . Stąd mamy ważne:
Twierdzenie 2.1. Suma dowolnej rodziny relacji z do jest relacją z do .
Dla takiej relacji, mamy: , dla pewnej relacji
Tzn. dwa elementy są ze sobą w relacji , gdy są z sobą w relacji , dla pewnej relacji z rodziny relacji
Podobnie możemy określić iloczyn rodziny relacji. Dla niepustej rodziny relacji z do , relacja , to taka relacja, że dwa elementy są ze sobą w relacji , gdy są z sobą w relacji , dla każdej relacji