Funkcje: Różnice pomiędzy wersjami
(→Funkcja różnowartościowa i 'na') |
(→Złożenie funkcji) |
||
| (Nie pokazano 7 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 15: | Linia 15: | ||
<math>X</math>-dowolny zbiór, <math>Y=\left\{ 0,1\right\}. </math> Relacja <math>X\times\left\{ 0\right\}</math> jest funkcją, ale nie jest już funkcją relacja <math>X\times\left\{ 0,1\right\}</math> jeśli tylko zbiór <math>X</math> jest niepusty. Wystarczy bowiem wyciągnąć z niepustego zbioru <math>X</math> element pewien <math>x\in X</math>, i utworzyć pary <math>\left( x,0\right) ,\left( x,1\right) </math>, co pokazuje, że elementowi <math>x</math> przypisaliśmy dwie wartości, a więc nie jest to funkcja. | <math>X</math>-dowolny zbiór, <math>Y=\left\{ 0,1\right\}. </math> Relacja <math>X\times\left\{ 0\right\}</math> jest funkcją, ale nie jest już funkcją relacja <math>X\times\left\{ 0,1\right\}</math> jeśli tylko zbiór <math>X</math> jest niepusty. Wystarczy bowiem wyciągnąć z niepustego zbioru <math>X</math> element pewien <math>x\in X</math>, i utworzyć pary <math>\left( x,0\right) ,\left( x,1\right) </math>, co pokazuje, że elementowi <math>x</math> przypisaliśmy dwie wartości, a więc nie jest to funkcja. | ||
| + | |||
| + | Dla dowolnego zbioru <math>X</math> relacja <math>I_X</math> identyczności na <math>X</math> jest funkcją ze zbioru <math>X</math> w ten sam zbiór <math>X</math>. Aby to wykazać, to przypuśćmy, że <math>\left( x,x _{1} \right)\in I_X</math> i <math>\left( x,x _{2} \right)\in I_X</math>. Założenie <math>\left( x,x _{1} \right)\in I_X</math> oznacza, że <math>x=x_1</math>, podobnie założenie <math>\left( x,x _{2} \right)\in I_X</math> oznacza, że <math>x=x_2</math>; zatem <math>x_1=x_2</math>. Łatwo się też przekonać, że zgodnie z intuicją <math>\left( I_{X}\right) _{L}=X </math>. Zatem <math>I_X</math> jest funkcją z <math>X</math> w <math>X</math>. | ||
Dla funkcji wprowadzimy podstawowe oznaczenia. Rozważmy funkcję <math>f:X \rightarrow Y</math>. Zbiór <math>X</math> nazywamy dziedziną funkcji <math>f</math>, a zbiór <math>Y</math> nazywamy przeciwdziedziną funkcji <math>f</math>. Dla dowolnego <math>x\in X</math>, jedyny element <math>y</math>, dla którego <math>(x,y)\in f</math>, to oznaczamy go przez <math>f(x)</math>, podobnie fakt <math>(x,y)\in f</math> notujemy jako <math>f(x)=y.</math> Mówimy wtedy, że funkcja <math>f</math> przyporządkowuje elementowi <math>x</math> element <math>y</math>. Elementy <math>X</math> nazywamy argumentami funkcji <math>f</math>. Zbiór <math>f_P</math> nazywamy zbiorem wartości funkcji <math>f</math>, a jego elementy wartościami funkcji <math>f</math>. | Dla funkcji wprowadzimy podstawowe oznaczenia. Rozważmy funkcję <math>f:X \rightarrow Y</math>. Zbiór <math>X</math> nazywamy dziedziną funkcji <math>f</math>, a zbiór <math>Y</math> nazywamy przeciwdziedziną funkcji <math>f</math>. Dla dowolnego <math>x\in X</math>, jedyny element <math>y</math>, dla którego <math>(x,y)\in f</math>, to oznaczamy go przez <math>f(x)</math>, podobnie fakt <math>(x,y)\in f</math> notujemy jako <math>f(x)=y.</math> Mówimy wtedy, że funkcja <math>f</math> przyporządkowuje elementowi <math>x</math> element <math>y</math>. Elementy <math>X</math> nazywamy argumentami funkcji <math>f</math>. Zbiór <math>f_P</math> nazywamy zbiorem wartości funkcji <math>f</math>, a jego elementy wartościami funkcji <math>f</math>. | ||
| Linia 42: | Linia 44: | ||
Każda bijekcja pomiędzy dwoma zbiorami, dobiera elementy tych zbiorów w pary- zobacz ilustrację obok. | Każda bijekcja pomiędzy dwoma zbiorami, dobiera elementy tych zbiorów w pary- zobacz ilustrację obok. | ||
| + | |||
| + | == Obrazy i przeciwobrazy == | ||
| + | [[Plik:Obrazy.JPG|300px|thumb|right|Obraz zbioru przez funkcję]] | ||
| + | ''Dla dowolnych zbiorów <math>X,Y</math> oraz dowolnej funkcji <math>f:X\rightarrow Y</math>, i dla dowolnego zbioru <math>A\subset X</math> definiujemy zbiór: | ||
| + | |||
| + | <math>\stackrel{ \rightarrow }{f}\left( A\right)=\left\{ f(x)\Bigl| \ \ x\in A\right\}= \{y\in Y: \bigvee_{x\in A} f(x)=y\}=\left\{ f(x)\Bigl| \ \ x\in A\right\} .</math>'' | ||
| + | |||
| + | Dla dowolnego zbioru <math>A\subset X</math> zbiór <math>\stackrel{ \rightarrow }{f}\left( A\right)</math> nazywamy ''obrazem'' zbioru <math>A</math> przez funkcję <math>f</math>. Jest to zbiór wartości funkcji <math>f</math> liczonych dla argumentów ze zbioru <math>A</math>. Zobacz ilustrację obok. | ||
| + | |||
| + | Przykład: Niech <math>f:\mathbb{N} \rightarrow \mathbb{N}</math> będzie dana jako: <math>f\left( n\right)=2n.</math> Wtedy: <math>\stackrel{ \rightarrow }{f}\left( \mathbb{N}\right)</math> jest zbiorem liczb parzystych, <math>\stackrel{ \rightarrow }{f}\left( \left\{ 1,2\right\} \right)=\left\{ 2,4\right\}</math>, obrazem zbioru liczb parzystych przez funkcję <math>f</math> jest zbiór liczb naturalnych podzielnych przez <math>4</math>. | ||
| + | [[Plik:Przeciwobraz.JPG|300px|thumb|right|Przeciwobraz zbioru przez funkcję]] | ||
| + | |||
| + | W podobny sposób definiujemy przeciwobrazy zbiorów przez funkcję. ''Dla dowolnej funkcji <math>f:X\rightarrow Y</math> przeciwobrazem zbioru <math>B \subset Y</math> przez funkcję <math>f</math> nazwiemy zbiór tych elementów zbioru <math>X</math>, którym funkcja przypisuje wartości ze zbioru <math>B</math>. Czyli dla dowolnego zbioru <math>B \subset Y</math> definiujemy zbiór:'' | ||
| + | |||
| + | <math>\stackrel{ \rightarrow }{f ^{-1} }\left( B\right)=\left\{ x\in X\Bigl| \ \ f\left( x\right) \in B\right\}.</math> | ||
| + | |||
| + | który to zbiór nazywamy ''przeciwobrazem'' zbioru <math>B</math> przez funkcję <math>f</math>. Jest to zbiór tych argumentów, którym funkcja przypisuję wartości ze zbioru <math>B</math>. Zobacz ilustrację obok. | ||
| + | |||
| + | Przykład: Niech <math>f:\mathbb{N} \rightarrow \mathbb{N}</math> będzie dana jako: <math>f\left( n\right)=2n.</math> Wtedy: <math>\stackrel{ \rightarrow }{f ^{-1} }\left( \left\{ 1,2\right\} \right)=\left\{ 1\right\}</math>, przeciwobrazem zbioru liczb nieparzystych przez funkcję <math>f</math> jest zbiór pusty, przeciwobrazem zbioru liczb naturalnych podzielnych przez <math>4</math>, przez funkcję <math>f</math>, jest zbiór liczb parzystych. | ||
| + | |||
| + | Poniżej podaję prosty fakt. | ||
| + | |||
| + | ''Dla dowolnej funkcji <math>f:X \rightarrow Y</math>, oraz zbiorów <math>A,B\subset X</math>, zachodzi: | ||
| + | |||
| + | <math>A\subset B \rightarrow \stackrel{ \rightarrow }{f}\left( A\right) \subset \stackrel{ \rightarrow }{f}\left( B\right).</math>'' | ||
| + | |||
| + | Czyli jeśli na podzbiorach dziedziny <math>X</math> zachodzi inkluzja, to taka sama (zgodna) inkluzja występuje na odpowiadającym im obrazach. | ||
| + | |||
| + | Prosty dowód: | ||
| + | |||
| + | Załóżmy, że <math>A\subset B</math>. Pokazujemy, że <math>\stackrel{ \rightarrow }{f}\left( A\right) \subset \stackrel{ \rightarrow }{f}\left( B\right).</math> Niech <math>y\in\stackrel{ \rightarrow }{f}\left( A\right).</math> Oznacza to, że <math>y=f(x)</math>, przy pewnym <math>x\in A</math>. Ponieważ mamy założenie, że <math>A\subset B</math>, to <math>x\in B</math>, zatem <math>y=f(x)</math> przy <math>x\in B</math>, a zatem <math>y\in \stackrel{ \rightarrow }{f}\left( B\right)</math>, i <math>\stackrel{ \rightarrow }{f}\left( A\right) \subset \stackrel{ \rightarrow }{f}\left( B\right).\square</math> | ||
| + | |||
| + | Kolejny podstawowy fakt: | ||
| + | |||
| + | ''Dla dowolnej funkcji <math>f:X \rightarrow Y</math>, oraz zbiorów <math>A,B\subset X</math>, mamy: | ||
| + | |||
| + | <math>\stackrel{ \rightarrow }{f}\left( A \cup B\right) = \stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right) .</math>'' | ||
| + | |||
| + | Czyli obraz sumy dwóch podzbiorów dziedziny, taki obraz sumy jest równy sumie obrazów tych zbiorów. | ||
| + | |||
| + | Dowód: | ||
| + | |||
| + | Z poprzedniego faktu, który mówi, że branie obrazu jest zgodne z zawieraniem( inkluzją), otrzymujemy, że <math>\stackrel{ \rightarrow }{f}\left( A\right) \subset \stackrel{ \rightarrow }{f}\left( A\cup B\right).</math> oraz, że <math>\stackrel{ \rightarrow }{f}\left( B\right) \subset \stackrel{ \rightarrow }{f}\left( A \cup B\right).</math> Zatem zbiory <math>\stackrel{ \rightarrow }{f}\left( A\right) ,\stackrel{ \rightarrow }{f}\left( B\right)</math> są podzbiorami zbioru <math>\stackrel{ \rightarrow }{f}\left( A\cup B\right)</math>, więc również ich suma jest podzbiorem tego zbioru, czyli <math>\stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right) \subset \stackrel{ \rightarrow }{f}\left( A \cup B\right).</math> Aby pokazać inkluzję w drugą stronę, to niech <math>y\in\stackrel{ \rightarrow }{f}\left( A \cup B\right)</math>. Oznacza to, że <math>y=f(x)</math>, przy pewnym <math>x\in A \cup B</math>. Jeśli <math>x\in A</math>, to <math>y=f(x)</math> przy <math>x\in A</math>, zatem <math>y\in\stackrel{ \rightarrow }{f}\left( A\right)</math>, a jeśli <math>x\in B,</math> to <math>y=f(x)</math> przy <math>x\in B</math>, zatem <math>y\in\stackrel{ \rightarrow }{f}\left( B\right)</math>, zatem w obydwu przypadkach <math>y\in \stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right),</math> i <math>\stackrel{ \rightarrow }{f}\left( A \cup B\right) \subset \stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right)</math>, a więc <math>\stackrel{ \rightarrow }{f}\left( A \cup B\right) = \stackrel{ \rightarrow }{f}\left( A\right) \cup \stackrel{ \rightarrow }{f}\left( B\right). \square</math> | ||
| + | |||
| + | Jeszcze jeden prosty fakt: | ||
| + | |||
| + | ''Dla dowolnej funkcji <math>f:X \rightarrow Y</math>, mamy:<math>\stackrel{ \rightarrow }{f}\left( \left\{ \right\} \right)=\left\{ \right\} .</math>'' | ||
| + | |||
| + | Dowód: Gdyby <math>\stackrel{ \rightarrow }{f}\left( \left\{ \right\} \right) \neq \left\{ \right\}</math>, to istniałby element <math>y\in\stackrel{ \rightarrow }{f}\left( \left\{ \right\} \right)</math>, a więc <math>y=f(x),</math> przy <math>x\in\left\{ \right\}</math>, a więc <math>x\in\left\{ \right\}</math>-sprzeczność. <math>\square</math> | ||
| + | |||
| + | |||
| + | Dla dowolnej funkcji <math>f:X \rightarrow Y</math>, '''przeciwobrazy''' różnych zbiorów jednoelementowych są rozłączne. Aby się o tym przekonać, niech <math>y _{1},y _{2}\in Y,</math> będą różnymi elementami zbioru <math>Y</math>. Chcemy sprawdzić, że zbiory <math>\stackrel{ \rightarrow }{f ^{-1} }\left\{ y _{1} \right\}</math> oraz <math>\stackrel{ \rightarrow }{f ^{-1} }\left\{ y _{2} \right\} </math> są rozłączne, czyli nie mają wspólnych elementów. Gdyby miały wspólny element <math>x\in X</math>, to wtedy z definicji przeciwobrazu <math>f\left( x\right) \in \left\{ y _{1} \right\}</math> oraz <math>f\left( x\right) \in \left\{ y _{2} \right\}</math>, czyli <math>f(x)=y _{1}</math> oraz <math>f(x)=y _{2}</math>, co wobec różności elementów <math>y_1,y_2</math> daję sprzeczność z definicją funkcji. | ||
| + | |||
| + | == Złożenie funkcji == | ||
| + | [[Plik:Złożenia_funkcji.JPG|300px|thumb|right|Ilustracja złożenia funkcji]] | ||
| + | ''Niech <math>X,Y,Z</math> będą zbiorami, a <math>f:X \rightarrow \textbf{Y}</math> oraz <math>g:\textbf{Y} \rightarrow Z</math> dowolnymi funkcjami. Złożeniem funkcji <math>f</math> i <math>g</math> nazywamy funkcję <math>g\circ f</math> ( uwaga!- jest odwrócona kolejność) <math>g\circ f:X \rightarrow Z</math> określoną jako: | ||
| + | |||
| + | <math>\left( g\circ f\right)\left( x\right)=g\left( f\left( x\right) \right),\hbox{ dla dowolnego } x\in X.</math>'' | ||
| + | |||
| + | Przykład: Niech <math>f:\mathbb{N} \rightarrow \mathbb{N}</math> będzie dana jako:<math>f\left( n\right) =n+1</math>, a <math>g:\mathbb{N} \rightarrow P\left( \mathbb{N}\right)</math> będzie dana jako <math>g\left( n\right) =\left\{ n\right\}.</math> Wtedy <math>g\circ f:\mathbb{N} \rightarrow P\left( \mathbb{N}\right)</math> działa tak: | ||
| + | |||
| + | <math>\left( g\circ f\right)\left( n\right)=g\left( f\left( n\right) \right)=\left\{ n+1\right\}, \hbox{ dla dowolnej liczby naturalnej } n.</math> | ||
| + | |||
| + | Złożenie funkcji nie musi być przemienne. Na przykład niech <math>f:\mathbb{N} \rightarrow \mathbb{N}</math> będzie dana jako:<math>f\left( n\right) =n+1</math>, a <math>g:\mathbb{N} \rightarrow \mathbb{N}</math> będzie dana jako <math>g\left( n\right) = 2n.</math> Wtedy <math>g\circ f:\mathbb{N} \rightarrow \mathbb{N}</math> działa tak: | ||
| + | |||
| + | <math>\left( g\circ f\right)\left( n\right)=g\left( f\left( n\right) \right)=g\left( n+1\right)=2\left( n+1\right)=2n+2.</math> | ||
| + | |||
| + | Natomiast <math>f\circ g:\mathbb{N} \rightarrow \mathbb{N}</math> działa tak: | ||
| + | |||
| + | <math>\left( f\circ g\right)\left( n\right)=f\left( g\left( n\right) \right)=f\left( 2n\right)=2n+1 \neq 2n+2,</math> | ||
| + | |||
| + | zatem <math>g\circ f \neq f\circ g.</math> | ||
Aktualna wersja na dzień 22:07, 13 lut 2019
W tym rozdziale wprowadzamy pojęcie funkcji. W teorii zbiorów funkcje, są relacjami, które spełniają dodatkowy warunek jednoznaczności. A więc funkcja jako relacja jest zbiorem, którego elementami są pary uporządkowane.
Relację nazywamy funkcją ze zbioru w zbiór , jeśli ma poniższe własności:
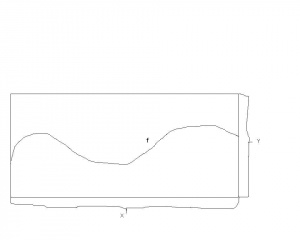
Czyli funkcja to relacja taka, że do każdego elementu ze zbioru można dobrać dokładnie jeden element będący z nim w relacji . Zobacz (uproszczoną) ilustrację obok- na przecięciu z każdym odcinkiem pionowym mamy dokładnie jeden element . Oczywiście rysunek jest uproszczony- wykres może być bardziej skomplikowany.
Dla zainteresowanych mogę dokładniej wyjaśnić definicję. Pierwsza własność mówi dokładnie tyle, że jeśli do jakiegoś elementu , możemy dobrać elementy i tak, aby obydwa były w relacji z , to muszą one być sobie równe, a więc do każdego elementu zbioru można dobrać co najwyżej jeden element, będący z nim w relacji . Druga własność mówi, że każdy element należy do , a więc do każdego elementu ze zbioru da się dobrać przynajmniej jeden element , będący z nim w relacji . Łącznie te dwa wnioski oznaczają, że do każdego elementu ze zbioru można dobrać dokładnie jeden element , będący z nim w relacji . Często będziemy używać skrótowego zapisu , który będzie oznaczał, że jest funkcją ze zbioru w zbiór Mówimy, że funkcja przekształca zbiór w zbiór . Zbiór wszystkich funkcji ze zbioru w zbiór , oznaczamy jako . Zbiór ten definiujemy jako:
Przykłady : relacja jest funkcją, ale już relacja funkcją nie jest, bo zerze przyporządkowuje dwie wartości- i .
-dowolny zbiór, Relacja jest funkcją, ale nie jest już funkcją relacja jeśli tylko zbiór jest niepusty. Wystarczy bowiem wyciągnąć z niepustego zbioru element pewien , i utworzyć pary , co pokazuje, że elementowi przypisaliśmy dwie wartości, a więc nie jest to funkcja.
Dla dowolnego zbioru relacja identyczności na jest funkcją ze zbioru w ten sam zbiór . Aby to wykazać, to przypuśćmy, że i . Założenie oznacza, że , podobnie założenie oznacza, że ; zatem . Łatwo się też przekonać, że zgodnie z intuicją . Zatem jest funkcją z w .
Dla funkcji wprowadzimy podstawowe oznaczenia. Rozważmy funkcję . Zbiór nazywamy dziedziną funkcji , a zbiór nazywamy przeciwdziedziną funkcji . Dla dowolnego , jedyny element , dla którego , to oznaczamy go przez , podobnie fakt notujemy jako Mówimy wtedy, że funkcja przyporządkowuje elementowi element . Elementy nazywamy argumentami funkcji . Zbiór nazywamy zbiorem wartości funkcji , a jego elementy wartościami funkcji .
Funkcja różnowartościowa i 'na'
Funkcję nazywamy różnowartościową, jeśli różnym argumentom przypisuje różne wartości, tzn. dla dowolnych , zachodzi:
Lub równoważnie
Powyższy warunek mówi, że jeśli funkcja argumentom przypisuje tą samą wartość, to te argumenty muszą być równe.
Przykłady: Funkcja dana jako: jest różnowartościowa. Kolejny przykład: funkcja, która każdej liczbie naturalnej przypisuję liczbę naturalną dwukrotnie większą jest różnowartościowa. Funkcja , dana jako: nie jest różnowartościowa. Podobnie dana jako: nie jest różnowartościowa, bo elementom przypisuję tą samą wartość- .Funkcja dana jako: nie jest różnowartościowa, bo
Funkcję nazywamy 'na' zbiór , gdy , tzn. gdy każdy element ze zbioru jest wartością funkcji na jakimś argumencie ze zbioru , czyli istnieje takie, że
A więc funkcja jest 'na' zbiór , gdy jej zbiór wartości jest całą przeciwdziedziną
Przykłady: funkcja , dana jako nie jest 'na' . Funkcja , dana jako jest 'na'. Kolejny przykład: Niech będzie ustalonym elementem. Funkcja dana jako; jest 'na'- jest stale równa
Funkcję nazywamy bijekcją (lub wzajemnie jednoznaczną), gdy jest różnowartościowa i 'na' zbiór
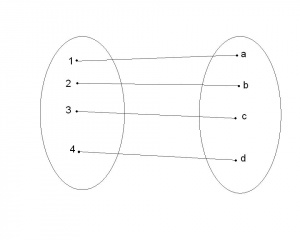
Każda bijekcja pomiędzy dwoma zbiorami, dobiera elementy tych zbiorów w pary- zobacz ilustrację obok.
Obrazy i przeciwobrazy
Dla dowolnych zbiorów oraz dowolnej funkcji , i dla dowolnego zbioru definiujemy zbiór:
Dla dowolnego zbioru zbiór nazywamy obrazem zbioru przez funkcję . Jest to zbiór wartości funkcji liczonych dla argumentów ze zbioru . Zobacz ilustrację obok.
Przykład: Niech będzie dana jako: Wtedy: jest zbiorem liczb parzystych, , obrazem zbioru liczb parzystych przez funkcję jest zbiór liczb naturalnych podzielnych przez .
W podobny sposób definiujemy przeciwobrazy zbiorów przez funkcję. Dla dowolnej funkcji przeciwobrazem zbioru przez funkcję nazwiemy zbiór tych elementów zbioru , którym funkcja przypisuje wartości ze zbioru . Czyli dla dowolnego zbioru definiujemy zbiór:
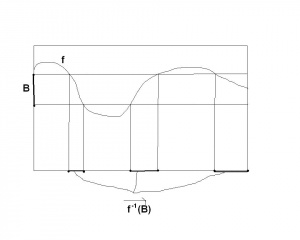
który to zbiór nazywamy przeciwobrazem zbioru przez funkcję . Jest to zbiór tych argumentów, którym funkcja przypisuję wartości ze zbioru . Zobacz ilustrację obok.
Przykład: Niech będzie dana jako: Wtedy: , przeciwobrazem zbioru liczb nieparzystych przez funkcję jest zbiór pusty, przeciwobrazem zbioru liczb naturalnych podzielnych przez , przez funkcję , jest zbiór liczb parzystych.
Poniżej podaję prosty fakt.
Dla dowolnej funkcji , oraz zbiorów , zachodzi:
Czyli jeśli na podzbiorach dziedziny zachodzi inkluzja, to taka sama (zgodna) inkluzja występuje na odpowiadającym im obrazach.
Prosty dowód:
Załóżmy, że . Pokazujemy, że Niech Oznacza to, że , przy pewnym . Ponieważ mamy założenie, że , to , zatem przy , a zatem , i
Kolejny podstawowy fakt:
Dla dowolnej funkcji , oraz zbiorów , mamy:
Czyli obraz sumy dwóch podzbiorów dziedziny, taki obraz sumy jest równy sumie obrazów tych zbiorów.
Dowód:
Z poprzedniego faktu, który mówi, że branie obrazu jest zgodne z zawieraniem( inkluzją), otrzymujemy, że oraz, że Zatem zbiory są podzbiorami zbioru , więc również ich suma jest podzbiorem tego zbioru, czyli Aby pokazać inkluzję w drugą stronę, to niech . Oznacza to, że , przy pewnym . Jeśli , to przy , zatem , a jeśli to przy , zatem , zatem w obydwu przypadkach i , a więc
Jeszcze jeden prosty fakt:
Dla dowolnej funkcji , mamy:
Dowód: Gdyby , to istniałby element , a więc przy , a więc -sprzeczność.
Dla dowolnej funkcji , przeciwobrazy różnych zbiorów jednoelementowych są rozłączne. Aby się o tym przekonać, niech będą różnymi elementami zbioru . Chcemy sprawdzić, że zbiory oraz są rozłączne, czyli nie mają wspólnych elementów. Gdyby miały wspólny element , to wtedy z definicji przeciwobrazu oraz , czyli oraz , co wobec różności elementów daję sprzeczność z definicją funkcji.
Złożenie funkcji
Niech będą zbiorami, a oraz dowolnymi funkcjami. Złożeniem funkcji i nazywamy funkcję ( uwaga!- jest odwrócona kolejność) określoną jako:
Przykład: Niech będzie dana jako:, a będzie dana jako Wtedy działa tak:
Złożenie funkcji nie musi być przemienne. Na przykład niech będzie dana jako:, a będzie dana jako Wtedy działa tak:
Natomiast działa tak:
zatem