Zbiory uporządkowane: Różnice pomiędzy wersjami
| Linia 41: | Linia 41: | ||
| + | [[Plik:Zbiory_uporządkowane-_funkcje.JPG|300px|thumb|right|]] | ||
Kolejny przykład. Niech <math>X</math> będzie niepustym ustalonym zbiorem. Niech <math>a,b\in\mathbb{R},</math> będą takie, że <math>a<b.</math> Niech <math>Y=\left[ a,b\right] \subset \mathbb{R}</math>. W zbiorze funkcji z <math>X</math> do <math>Y</math>, czyli <math>Y^X</math>, wprowadzamy relację <math>R</math>: | Kolejny przykład. Niech <math>X</math> będzie niepustym ustalonym zbiorem. Niech <math>a,b\in\mathbb{R},</math> będą takie, że <math>a<b.</math> Niech <math>Y=\left[ a,b\right] \subset \mathbb{R}</math>. W zbiorze funkcji z <math>X</math> do <math>Y</math>, czyli <math>Y^X</math>, wprowadzamy relację <math>R</math>: | ||
<math>f\left( R\right) g \Longleftrightarrow \hbox{ dla dowolnego } x\in X: f\left( x\right) \le g\left( x\right).</math> | <math>f\left( R\right) g \Longleftrightarrow \hbox{ dla dowolnego } x\in X: f\left( x\right) \le g\left( x\right).</math> | ||
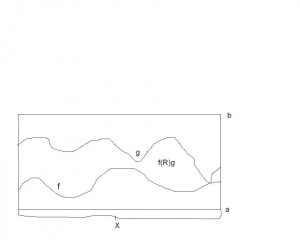
| − | Wykażemy, że <math>R</math> jest relacją porządku na <math>Y^X</math>. | + | Wykażemy, że <math>R</math> jest relacją porządku na <math>Y^X</math>. Geometrycznie ten porządek oznacza, że funkcja <math>f</math> jest mniejsza od funkcji <math>g</math>, gdy wykres funkcji <math>f</math> w każdym punkcie leży poniżej (lub na równi) niż wykres funkcji <math>g</math> (zobacz ilustrację obok). |
Zwrotność. Niech <math>f\in \left( Y=\left[ a,b\right]\right) ^{X}</math>. Niech <math>x\in X</math>. Wtedy niewątpliwie <math>f\left( x\right)=f\left( x\right)</math>, a więc ze zwrotności naturalnego porządku na liczbach rzeczywistych <math>f\left( x\right) \le f\left( x\right)</math>, Z dowolności wyboru <math>x\in X</math>, oznacza to, że <math>f\left( R\right) f</math>. Relacja <math>R</math> jest więc zwrotna. | Zwrotność. Niech <math>f\in \left( Y=\left[ a,b\right]\right) ^{X}</math>. Niech <math>x\in X</math>. Wtedy niewątpliwie <math>f\left( x\right)=f\left( x\right)</math>, a więc ze zwrotności naturalnego porządku na liczbach rzeczywistych <math>f\left( x\right) \le f\left( x\right)</math>, Z dowolności wyboru <math>x\in X</math>, oznacza to, że <math>f\left( R\right) f</math>. Relacja <math>R</math> jest więc zwrotna. | ||
Wersja z 04:38, 9 cze 2018
Zbiorem uporządkowanym (częściowo) nazywamy parę , gdzie jest zbiorem, a jest relacją:
1. Zwrotną, tzn. dla dowolnego zachodzi
2. Antysymetryczną, tzn. spełnia warunek
3. Przechodnią, tzn. spełnia warunek
Jeżeli dodatkowo relacja jest spójna, tzn. dla dowolnych zachodzi lub , to wtedy parę , nazywamy zbiorem liniowo uporządkowanym. Mówimy wtedy, że jest liniowym porządkiem na , oraz że zbiór jest liniowo uporządkowany przez . Podobnie dla zbioru uporządkowanego, relację nazywamy porządkiem (częściowym) na zbiorze
Często oznaczamy relację porządku przez ( lub symbolami podobnymi np.). Dla zbioru uporządkowanego , dla dowolnego zachodzi bo relacja porządku jest zwrotna. Zatem dla elementów , oznaczamy gdy i i mówimy, że jest silnie mniejszy od Podobnie dla innych oznaczeń relacji porządku. W zbiorze uporządkowanym , będziemy czasem pisać zamiast , oraz zamiast
Warto zobaczyć jaką postać przyjmują wymagania stawiane zbiorom liniowo uporządkowanym, gdy relację liniowego porządku oznaczymy przez , (i gdy będziemy pisać zamiast będziemy pisać O zwrotności już pisałem, jako , dla dowolnego Antysymetria przyjmuję postać: jeżeli i , to . Przechodniość przyjmuję postać: jeżeli i , to Spójność zapisujemy jako: dla dowolnych ma zachodzić lub . Nietrudno więc zauważyć, że te własności są spełnione w zbiorach liczbowych z naturalnym porządkiem. Nasza definicja zbioru liniowego uporządkowanego jest więc uogólnieniem znanych własności porządkowych na zbiorach liczbowych. Nie zapominajmy jednak, że formalnie jest to zbiór wraz z relacją, która ma dokładnie wymienione własności.
Niech będzie zbiorem uporządkowanym. niech . Element nazywamy elementem najmniejszym zbioru względem porządku , gdy , oraz gdy dla dowolnego , zachodzi
Tzn. element najmniejszy zbioru , to taki element , który jest mniejszy lub równy (względem rozpatrywanego porządku) od każdego elementu tego zbioru .
Analogicznie możemy zdefiniować element największy zbioru , jako taki element , który jest większy lub równy od każdego elementu tego zbioru, tzn. dla dowolnego zachodzi
Przykład: Rozważmy zbiór liczb naturalnych uporządkowany ( to należy pokazać) relacją podzielności |, tzn.
Równoważnie to oznacza, że (dla ) iloraz jest pewną liczbą naturalną . Wykażemy, że jest zbiorem uporządkowanym, a potem, że jest elementem największym, a jest elementem najmniejszym (tak przekornie wychodzi- ale nie względem naturalnego porządku, tylko względem naszego porządku ).
Zwrotność. Niech Wtedy możemy dobrać , i otrzymać , a więc . Relacja jest więc zwrotna (zwróć uwagę co się dzieje dla , jak działa to proste rozumowanie).
Przechodniość. Niech będą takie, że oraz, że . Pokażemy, że . Nasze założenia oznaczają, że dla pewnej liczby naturalnej , oraz, że dla pewnej liczby naturalnej . Wobec czego Ponieważ iloczyn dwóch liczb naturalnych jest liczbą naturalną, więc możemy dobrać , tak aby , a więc
Antysymetria. Weźmy dowolne liczby naturalne , dla których i Nasze założenia oznaczają, że dla pewnej liczby naturalnej , oraz, że dla pewnej liczby naturalnej Wobec czego
Rozważymy teraz dwa przypadki. Jeśli , to wtedy , a więc z prawa skreśleń dla liczb naturalnych otrzymujemy, że , i ponieważ są to liczby naturalne, to , a więc , czyli .
Jeśli , to wtedy , czyli , więc Relacja jest więc antysymetryczna.
Zatem jest zbiorem uporządkowanym. W tym zbiorze uporządkowanym elementem największym jest , a najmniejszym .
Niech . Wtedy możemy dobrać , i otrzymać , a więc . Ponieważ każda liczba naturalna dzieli (czyli każda liczba naturalna jest mniejsza, względem relacji podzielności, od ), to jest elementem największym (względem - relacji podzielności.) W tym zbiorze uporządkowanym jest elementem najmniejszym. Niech . Wtedy możemy dobrać , i otrzymać , a więc . Ponieważ dzieli każdą liczbę naturalną (czyli jest mniejszy, względem relacji podzielności, od każdej liczby), to jest elementem najmniejszym.
Kolejny przykład. Niech będzie niepustym ustalonym zbiorem. Niech będą takie, że Niech . W zbiorze funkcji z do , czyli , wprowadzamy relację :
Wykażemy, że jest relacją porządku na . Geometrycznie ten porządek oznacza, że funkcja jest mniejsza od funkcji , gdy wykres funkcji w każdym punkcie leży poniżej (lub na równi) niż wykres funkcji (zobacz ilustrację obok).
Zwrotność. Niech . Niech . Wtedy niewątpliwie , a więc ze zwrotności naturalnego porządku na liczbach rzeczywistych , Z dowolności wyboru , oznacza to, że . Relacja jest więc zwrotna.
Antysymetria. Załóżmy, że i . Zatem dla dowolnego mamy oraz dla każdego , mamy Niech Wtedy oraz Z antysymetrii naturalnego porządku na liczbach rzeczywistych, otrzymujemy, że , Z dowolności wyboru , oznacza to, że . Relacja jest więc antysymetryczna.
Przechodniość. Załóżmy, że i . Zatem dla dowolnego mamy oraz dla każdego , mamy Niech Wtedy oraz Z przechodniości porządku otrzymujemy, że , Z dowolności wyboru , oznacza to, że . Relacja jest więc przechodnia.
Zatem jest zbiorem uporządkowanym. Elementem najmniejszym jest funkcja stale równa , a elementem największym funkcja stale równa , tzn.
Mamy bowiem, dla dowolnej funkcji z do , oraz dla dowolnego (bo są to funkcje o wartościach w ), mamy , a więc , zatem ( z dowolności ) , oraz , czyli jest elementem najmniejszym, oraz jest elementem największym.
Niech zbiory uporządkowane. Porządek nazywamy rozszerzeniem porządku , gdy dla dowolnych spełniony jest warunek:
Tzn. jeśli jest mniejszy ( lub równy) od względem danego porządku (na ),to tymbardziej musi być mniejsze(lub równe) od względem porządku rozszerzającego. Dla liniowych porządków wygląda to tak, że porządek rozszerzający jest szerszy- zobacz ilustrację obok.
Twierdzenie:
Niech będzie dowolnym ustalonym zbiorem. Niech będzie pewnym zbiorem złożonym z liniowych porządków( samych relacji) określonych na pewnych podzbiorach , takim, że dla dowolnych dwóch liniowych porządków w jeden jest rozszerzeniem drugiego, to wtedy dla relacji , zachodzi i jest liniowym porządkiem na tym zbiorze.
Tzn. suma rodziny liniowych porządków na podzbiorach , i jeśli wiemy, że dla dowolnych dwóch takich liniowych porządków jeden jest rozszerzeniem drugiego, to wtedy suma rodziny takich liniowych porządków jest liniowym porządkiem na swoim polu- zobacz ilustrację obok.
Dowód:
Aby wykazać, że wykażemy inkluzję w obydwie strony.
Aby pokazać, że , to niech . Oznacza to , że przy pewnym . To z kolei zapisujemy a więc dla pewnego liniowego porządku z . Porządek taki jest zwrotny, więc , a więc otrzymujemy, że , lub inaczej , i ponieważ jest prawą współrzędna pary z relacji , to , i
Dowód inkluzji w drugą stronę jest analogiczny. A więc Oznaczmy ten zbiór jako . Wykażemy, że jest liniowym porządkiem na tym zbiorze.
Zwrotność. Niech . Należy pokazać, że , lub inaczej że czyli, że dla pewnego liniowego porządku z . Ale każdy liniowy porządek jest zwrotny, więc powyższy fakt jest prawdziwy. Relacja jest więc zwrotna.
Antysymetria. Niech i . Pokażemy, że . Równoważnie możemy zapisać nasze założenia jako i Pierwszy warunek oznacza, że dla pewnego liniowego porządku z Drugi warunek oznacza, że dla pewnego liniowego porządku z ( niekoniecznie tego samego). Ale wiemy, że dla dowolnych dwóch liniowych porządków z jeden jest rozszerzeniem drugiego, więc jeśli jest rozszerzeniem , to z warunku wynika, że mamy , i ponieważ liniowy porządek jest antysymetryczny, to dostajemy , co należało pokazać. W drugim przypadku jest rozszerzeniem , i wtedy z warunku wynika, że , mamy , i ponieważ liniowy porządek jest antysymetryczny, to dostajemy , co należało pokazać. Antysymetria jest więc pokazana.
Przechodniość. Niech Pokażemy, że Nasze założenia możemy inaczej zapisać jako: oraz Wnioskujemy, że dla pewnego liniowego porządku z , oraz, że dla pewnego liniowego porządku z . Dla porządków , jeden jest rozszerzeniem drugiego, więc jeśli jest rozszerzeniem , to z faktu wynika, że , mamy, że , więc z przechodniości liniowego porządku otrzymujemy, że , a więc , czyli W pozostałym przypadku musi być rozszerzeniem , a wtedy z faktu wynika, że , mamy założenie, że , więc z przechodniości liniowego porządku , dostajemy, że , i również w tym przypadku Relacja jest więc przechodnia.
Dowód spójności jest niestety bardzo żmudny, więc go pomijamy. Wykazaliśmy, że jest porządkiem na swoim polu. Tego twierdzenia użyjemy tylko chyba raz w dowodzie twierdzenia Zermelo. To, że ten porządek jest liniowy nie będzie nam wtedy konieczne.