Naiwna teoria mnogości: Różnice pomiędzy wersjami
(→OPERACJE NA ZBIORACH:) |
|||
| (Nie pokazano 5 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
Teoria zbiorów, zwana również teorią mnogości, została stworzona około połowy XIX wieku, przez niemieckiego matematyka Georga Cantora. Teoria mnogości to gałąź matematyki zajmująca się zbiorami - kolekcją obiektów. | Teoria zbiorów, zwana również teorią mnogości, została stworzona około połowy XIX wieku, przez niemieckiego matematyka Georga Cantora. Teoria mnogości to gałąź matematyki zajmująca się zbiorami - kolekcją obiektów. | ||
| − | Według Cantora każda kolekcja obiektów jest zbiorem. Wtedy te obiekty nazywamy elementami zbioru; i jeśli obiekt <math>a</math> jest elementem zbioru <math>A</math>, to zapisujemy to jako <math>a\in A</math>. Czytamy to również jako: element <math>a</math> należy do zbioru <math>A</math>. W przeciwnym przypadku, jeśli obiekt <math>a</math> nie jest elementem zbioru <math>A</math>, to zapisujemy to jako <math>a\not\in A</math>, i czytamy: <math>a</math> nie należy do zbioru <math>A</math>, albo <math>a</math> nie jest elementem zbioru <math>A</math>. Skończone zbiory można definiować po przez wypisanie ich elementów (w nawiasach klamrowych na oznaczenie zbioru). | + | Według Cantora każda kolekcja obiektów jest zbiorem. Wtedy te obiekty nazywamy elementami zbioru; i jeśli obiekt <math>a</math> jest elementem zbioru <math>A</math>, to zapisujemy to jako <math>a\in A</math>. Czytamy to również jako: element <math>a</math> należy do zbioru <math>A</math>. W przeciwnym przypadku, jeśli obiekt <math>a</math> nie jest elementem zbioru <math>A</math>, to zapisujemy to jako <math>a\not\in A</math>, i czytamy: <math>a</math> nie należy do zbioru <math>A</math>, albo <math>a</math> nie jest elementem zbioru <math>A</math>. Zbiory na ogół oznaczamy dużymi literami, np. <math>A,B,X</math>. Skończone zbiory można definiować po przez wypisanie ich elementów (w nawiasach klamrowych na oznaczenie zbioru). Np. zbiór <math>A=\left\{ 0,1,5\right\}</math> posiada trzy elementy: <math>0,1</math> i <math>5</math>. Zgodnie z powyższym możemy to zapisać <math>0\in A</math>, i przeczytać <math>0</math> należy do zbioru <math>A</math>, albo <math>0</math> jest elementem zbioru <math>A</math>. Podobnie możemy zapisać <math>5\in A, 1\in A</math>. Ale już np. <math>2\not\in A</math>- <math>2</math> nie jest elementem zbioru <math>A</math>. Inny przykład- "Kraków" <math>\in</math> "zbiór wszystkich miast Polski", bo Kraków jest miastem Polski. Aby zdefiniować zbiór, należy określić sposób rozpoznawania czy dany obiekt jest jest jego elementem, czy nie. Musimy wiedzieć z jakich elementów jest on złożony, a inne obiekty nie są jego elementami. |
| − | + | Dwa zbiory są sobie równe (takie same), jeśli posiadają dokładnie te same elementy. Jedynymi elementami zbioru <math>\{2,3\}</math> są liczby naturalne <math>2</math> i <math>3</math>, tą samą własność ma zbiór <math>\{3,2\}</math>, a więc <math>\{2,3\}=\{3,2\}</math>, ale również <math>\{2,3\}=\{2,2,3\}</math>, bo ostatni zbiór też ma dokładnie elementy <math>2</math> i <math>3</math>, oraz <math>\{2,3\}=</math> "zbiór liczb naturalnych ściśle pomiędzy <math>1</math> a <math>4</math>". W definicji zbioru nie ma znaczenia kolejność, w jakiej wymienione są jego elementy, ani to czy element się powtarza w zbiorze. | |
| − | |||
| − | + | Zbiory można definiować na wiele sposobów. Najprostszym sposobem jest wypisanie jego elementów. Strategia ta zawodzi jednak w odniesieniu do zbiorów nieskończonych - nie jesteśmy w stanie wypisać wszystkich liczb naturalnych. Zbiór liczb naturalnych zapisujemy nieformalnie jako: <math> \mathbb{N}=\left\{ 0,1,2,3,\ldots\right\}.</math> Podobnie, zbiór liczb naturalnych parzystych zapisujemy jako: <math> \left\{ 0,2,4,6,8,\ldots\right\}. </math> Przed wielokropkiem należy wypisać co najmniej tyle początkowych elementów, tak aby nie wprowadzać nieporozumień, żeby nikt nie zrozumiał (i to poprawnie) inaczej ten zbiór niż chcemy. | |
| − | + | Innym sposobem definiowania zbiorów jest rozważanie zbioru wszystkich elementów spełniających daną własność. Na przykład zbiór liczb parzystych może być zdefiniowany jako: <math> A=\left\{ x \Bigl | \ \ x \hbox{ jest liczbą parzystą } \right\} </math> Np. <math> 2\in A </math>, bo <math> 2 </math> jest liczbą parzystą. Bardziej ogólnie, definicje te wyglądają tak: <math>\left\{ x \Bigl | \ \ \hbox{ warunek} \right\}</math>. W skład powyższego zbioru wchodzą dokładnie te elementy, które spełniają warunek pojawiający się w definicji tegoż zbioru. Kolejny przykład: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Innym sposobem definiowania zbiorów jest rozważanie zbioru wszystkich elementów spełniających daną własność. Na przykład zbiór liczb parzystych może być zdefiniowany jako: | ||
| − | |||
| − | <math> A=\left\{ x \Bigl | \ \ x \hbox{ jest liczbą parzystą } \right\} </math> | ||
| − | |||
| − | Np. <math> 2\in A </math>, bo <math> 2 </math> jest liczbą parzystą. | ||
| − | |||
| − | Bardziej ogólnie, definicje te wyglądają tak: | ||
| − | |||
| − | <math>\left\{ x \Bigl | \ \ \hbox{ warunek} \right\}</math>. | ||
| − | |||
| − | W skład powyższego zbioru wchodzą dokładnie te elementy, które spełniają warunek pojawiający się w definicji tegoż zbioru. | ||
| − | |||
| − | Kolejny przykład | ||
<math>\hbox{ POLSKA } =\left\{ x \Bigl | \ \ x \hbox{ jest miastem Polski } \right\}</math> , | <math>\hbox{ POLSKA } =\left\{ x \Bigl | \ \ x \hbox{ jest miastem Polski } \right\}</math> , | ||
| − | <math>\hbox{ Kraków } \in \hbox{ POLSKA }</math>, bo Kraków jest miastem Polski. | + | <math>\hbox{ Kraków } \in \hbox{ POLSKA }</math>, bo Kraków jest miastem Polski. <math>\hbox{ Berlin} \not\in \hbox{ POLSKA }</math>, bo Berlin nie leży w Polsce. |
| − | |||
| − | <math>\hbox{ Berlin} \not\in \hbox{ POLSKA }</math>, bo Berlin nie leży w Polsce. | ||
| − | |||
== Inkluzja, równość zbiorów: == | == Inkluzja, równość zbiorów: == | ||
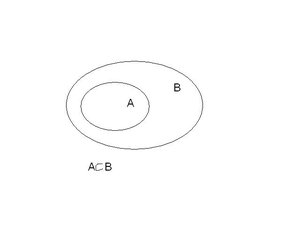
| − | Pomiędzy zbiorem liczb parzystych a zbiorem wszystkich liczb naturalnych występuje oczywista zależność. Każda liczba parzysta jest liczbą naturalną, co, ujęte w języku zbiorów, oznacza, że każdy element zbioru liczb parzystych jest elementem zbioru liczb naturalnych. Zbiór liczb parzystych jest podzbiorem zbioru liczb naturalnych. Ogólniej, dla dwóch zbiorów <math>A</math>, <math>B</math>, jeśli każdy element zbioru <math>A</math> jest elementem zbioru <math>B</math>, to nazywamy to zawieraniem zbiorów, i czytamy: zbiór <math>A</math> zawiera się w zbiorze <math>B</math>, co zapisujemy <math>A \subset B</math>. | + | Pomiędzy zbiorem liczb parzystych a zbiorem wszystkich liczb naturalnych występuje oczywista zależność. Każda liczba parzysta jest liczbą naturalną, co, ujęte w języku zbiorów, oznacza, że każdy element zbioru liczb parzystych jest elementem zbioru liczb naturalnych. Zbiór liczb parzystych jest podzbiorem zbioru liczb naturalnych. Ogólniej, dla dwóch zbiorów <math>A</math>, <math>B</math>, jeśli każdy element zbioru <math>A</math> jest elementem zbioru <math>B</math>, to nazywamy to zawieraniem zbiorów, i czytamy: zbiór <math>A</math> zawiera się w zbiorze <math>B</math>, co zapisujemy <math>A \subset B</math>. Mówimy wtedy też, że zbiór <math>A</math> jest podzbiorem zbioru <math>B</math> ( <math>B</math> jest nadzbiorem <math>A</math>). Zawieranie zbiorów nazywane jest też inkluzją.[[Plik:Inkluzja.jpg|300px| thumb|right|Inkluzja ]] |
| − | Mówimy wtedy też, że zbiór <math>A</math> jest podzbiorem zbioru <math>B</math> ( <math>B</math> jest nadzbiorem <math>A</math>). Zawieranie zbiorów nazywane jest też inkluzją. | + | Np.: <math>\left\{ 1,2\right\} \subset \left\{ 1,2,3\right\}</math>, ale też <math>\left\{ 1,2\right\} \subset \left\{ 1,2\right\}</math> oraz "zbiór wszystkich psów" <math>\subset</math> "zbiór wszystkich zwierząt". |
| − | |||
| − | [[Plik:Inkluzja.jpg|300px]] | ||
| − | + | Dla dowolnego zbioru <math>A</math>, mamy: <math>A \subset A</math> (bo każdy element zbioru <math>A</math>, jest elementem <math>A</math>). Wspomnieliśmy wcześniej, że dwa zbiory są sobie równe, wtedy i tylko wtedy, kiedy posiadają dokładnie takie same elementy. Nawiązuje do tego poniższe twierdzenie: | |
| − | |||
| − | |||
| − | Dla dowolnego zbioru <math>A</math>, mamy: <math>A \subset A</math> (bo każdy element zbioru <math>A</math>, jest elementem <math>A</math>). | ||
| − | Wspomnieliśmy wcześniej, że dwa zbiory są sobie równe, wtedy i tylko wtedy, kiedy posiadają dokładnie takie same elementy. Nawiązuje do tego poniższe twierdzenie: | ||
<math>A=B, \hbox { wtedy i tylko wtedy, gdy: } A \subset B \hbox{ i }B \subset A.</math> | <math>A=B, \hbox { wtedy i tylko wtedy, gdy: } A \subset B \hbox{ i }B \subset A.</math> | ||
| Linia 77: | Linia 39: | ||
== OPERACJE NA ZBIORACH: == | == OPERACJE NA ZBIORACH: == | ||
| − | |||
'''Sumą''' dwóch zbiorów <math>A,B</math>, to zbiór oznaczany jako ''<math>A \cup B</math>'', złożony dokładnie ze wszystkich elementów zbioru <math>A</math>, oraz ze wszystkich elementów zbioru <math>B</math>. | '''Sumą''' dwóch zbiorów <math>A,B</math>, to zbiór oznaczany jako ''<math>A \cup B</math>'', złożony dokładnie ze wszystkich elementów zbioru <math>A</math>, oraz ze wszystkich elementów zbioru <math>B</math>. | ||
| Linia 83: | Linia 44: | ||
Np. <math>\left\{ 1,2\right\} \cup \left\{ 2,3\right\} =\left\{ 1,2,3\right\}</math>. | Np. <math>\left\{ 1,2\right\} \cup \left\{ 2,3\right\} =\left\{ 1,2,3\right\}</math>. | ||
| − | [[ Plik:Suma dwoch zbiorow.jpeg|300px]] | + | [[ Plik:Suma dwoch zbiorow.jpeg|300px|thumb|right| Suma dwóch zbiorów]] |
'''Iloczynem (częścią wspólną, przekrojem )''', dwóch zbiorów <math>A,B</math>, to zbiór oznaczany jako ''<math>A \cap B</math>'', złożony dokładnie z tych elementów zbioru <math>A</math>, które jednocześnie są elementami zbioru <math>B</math>. | '''Iloczynem (częścią wspólną, przekrojem )''', dwóch zbiorów <math>A,B</math>, to zbiór oznaczany jako ''<math>A \cap B</math>'', złożony dokładnie z tych elementów zbioru <math>A</math>, które jednocześnie są elementami zbioru <math>B</math>. | ||
| − | Np. <math>\left\{ 1,2,3\right\} \cap \left\{ 2,3,4\right\} =\left\{ 2,3\right\}</math> | + | Np. <math>\left\{ 1,2,3\right\} \cap \left\{ 2,3,4\right\} =\left\{ 2,3\right\}</math>, <math>\left\{ 1,2\right\} \cap \left\{ 3,4\right\} =\left\{ \right\}</math>- zbiór nieposiadający elementów, zwany dalej zbiorem pustym. |
| − | [[Plik:Iloczyn dwóch zbiorow.JPG|300px|thumb| | + | [[Plik:Iloczyn dwóch zbiorow.JPG|300px|thumb|right|Iloczyn dwóch zbiorów]] |
'''Różnicą''' dwóch zbiorów <math>A,B</math>, to zbiór oznaczany jako ''<math>A \setminus B</math>'', złożony dokładnie z tych elementów zbioru <math>A</math>, które nie są elementami zbioru <math>B</math>. | '''Różnicą''' dwóch zbiorów <math>A,B</math>, to zbiór oznaczany jako ''<math>A \setminus B</math>'', złożony dokładnie z tych elementów zbioru <math>A</math>, które nie są elementami zbioru <math>B</math>. | ||
| − | Np. <math>\left\{ 1,2,3\right\} \setminus \left\{ 2,3,4\right\} =\left\{ 1\right\}</math> | + | Np. <math>\left\{ 1,2,3\right\} \setminus \left\{ 2,3,4\right\} =\left\{ 1\right\}</math>, <math>\left\{ 1,2\right\} \setminus \left\{ 3,4\right\} =\left\{ 1,2\right\}</math>. |
| + | [[Plik: Różnica dwóch zbiorów.JPG|300px|thumb|right|Różnica dwóch zbiorów]] | ||
| + | |||
'''Fakt.''' Jeśli mamy, że <math>A \subset B</math>, to wtedy: | '''Fakt.''' Jeśli mamy, że <math>A \subset B</math>, to wtedy: | ||
| Linia 103: | Linia 66: | ||
<math>3. \ \ A \setminus B=\left\{ \right\}</math>. | <math>3. \ \ A \setminus B=\left\{ \right\}</math>. | ||
| − | Np.: <math>\left\{ 1,2\right\} \cup \left\{ 1,2,3\right\}=\left\{ 1,2,3\right\}</math> | + | Np.: <math>\left\{ 1,2\right\} \cup \left\{ 1,2,3\right\}=\left\{ 1,2,3\right\}</math>, <math>\left\{ 1,2\right\} \cap \left\{ 1,2,3 \right\} =\left\{ 1,2\right\}</math>. |
| − | |||
| − | <math>\left\{ 1,2\right\} \cap \left\{ 1,2,3 \right\} =\left\{ 1,2\right\}</math>. | ||
Dla dowolnego zbioru <math>A</math>, zachodzi: <math>A \cup A=A</math>, oraz <math>A \cap A=A</math>. <math>A \cup A</math>- jest to zbiór złożony ze wszystkich elementów zbioru <math>A</math>, oraz ze wszystkich elementów zbioru <math>A</math>, czyli ze wszystkich elementów zbioru <math>A</math>, co potwierdza równość <math>A \cup A=A</math>. Natomiast <math>A \cap A</math>- jest to zbiór złożony dokładnie z tych elementów zbioru <math>A</math>, które są elementami zbioru <math>A</math>, czyli ze wszystkich elementów zbioru <math>A</math>, co potwierdza równość <math>A \cap A=A</math>. | Dla dowolnego zbioru <math>A</math>, zachodzi: <math>A \cup A=A</math>, oraz <math>A \cap A=A</math>. <math>A \cup A</math>- jest to zbiór złożony ze wszystkich elementów zbioru <math>A</math>, oraz ze wszystkich elementów zbioru <math>A</math>, czyli ze wszystkich elementów zbioru <math>A</math>, co potwierdza równość <math>A \cup A=A</math>. Natomiast <math>A \cap A</math>- jest to zbiór złożony dokładnie z tych elementów zbioru <math>A</math>, które są elementami zbioru <math>A</math>, czyli ze wszystkich elementów zbioru <math>A</math>, co potwierdza równość <math>A \cap A=A</math>. | ||
| Linia 111: | Linia 72: | ||
== Zbiory złożone ze zbiorów i inne podstawowe sprawy:== | == Zbiory złożone ze zbiorów i inne podstawowe sprawy:== | ||
| − | Elementami zbiorów mogą być inne zbiory, np.: <math>A=\left\{ \ \ \left\{ \right\}, \left\{ 0\right\}, \ \left\{ \left\{ \left\{ 1\right\} \right\} \right\}, \ \ \left\{ \left\{ \left\{ 2\right\} \right\} \right\}, \ \ \left\{ \left\{ 5\right\} \right\} \ \ \right\}</math>. Ten zbiór posiada <math>5</math> elementów, np. <math>\left\{ \left\{ \left\{ 1\right\} \right\} \right\} \in A</math>. Oczywiście, <math> \left\{ 1\right\}</math> to zbiór jednoelementowy złożony z <math>1</math>, dalej <math>\left\{ \left\{ 1\right\} \right\} </math> to zbiór jednoelementowy złożony z elementu <math> \left\{ 1\right\}</math>- poprzedniego zbioru, i <math>\left\{ \left\{ \left\{ 1\right\} \right\} \right\}</math> to zbiór jednoelementowy złożony z poprzedniego elementu, mamy <math>\left\{ \left\{ 1\right\} \right\} \in \left\{ \left\{ \left\{ 1\right\} \right\} \right\}</math>. Podobnie, <math>\left\{ \left\{ \left\{ 2\right\} \right\} \right\}\in A</math>, oraz <math>\left\{ \right\}\in A</math>. Takie zbiory (złożone ze zbiorów) nazywamy rodzinami zbiorów. Zgodnie ze założeniami Cantora -każda kolekcja obiektów jest zbiorem. Możemy zatem mówić, np. o zbiorze złożonym ze funkcji, a także o dowolnym zbiorze dwuelementowym (np. takim, którego pierwszym elementem jest pewna liczba, a drugim pewien zbiór). Elementy zbioru nie muszą mieć tej samej natury. Podkreślmy jeszcze, że poprawnie utworzony zbiór ( jest to pewien obiekt matematyczny)- a więc jeden element (zbiór)- złożony z elementów, ale sam w sobie jest jednym zbiorem. Zbiory, gdy mają takie same elementy, to są równe, a więc jest to jeden i ten sam zbiór. | + | Elementami zbiorów mogą być inne zbiory, np.: <math>A=\left\{ \ \ \left\{ \right\}, \left\{ 0\right\}, \ \left\{ \left\{ \left\{ 1\right\} \right\} \right\}, \ \ \left\{ \left\{ \left\{ 2\right\} \right\} \right\}, \ \ \left\{ \left\{ 5\right\} \right\} \ \ \right\}</math>. Ten zbiór posiada <math>5</math> elementów, np. <math>\left\{ \left\{ \left\{ 1\right\} \right\} \right\} \in A</math>. Oczywiście, <math> \left\{ 1\right\}</math> to zbiór jednoelementowy złożony z <math>1</math>, dalej <math>\left\{ \left\{ 1\right\} \right\} </math> to zbiór jednoelementowy złożony z elementu <math> \left\{ 1\right\}</math>- poprzedniego zbioru, i <math>\left\{ \left\{ \left\{ 1\right\} \right\} \right\}</math> to zbiór jednoelementowy złożony z poprzedniego elementu, mamy <math>\left\{ \left\{ 1\right\} \right\} \in \left\{ \left\{ \left\{ 1\right\} \right\} \right\}</math>. Podobnie, <math>\left\{ \left\{ \left\{ 2\right\} \right\} \right\}\in A</math>, oraz <math>\left\{ \right\}\in A</math>. Takie zbiory (złożone ze zbiorów) nazywamy czasem rodzinami zbiorów. Zgodnie ze założeniami Cantora -każda kolekcja obiektów jest zbiorem. Możemy zatem mówić, np. o zbiorze złożonym ze funkcji, a także o dowolnym zbiorze dwuelementowym (np. takim, którego pierwszym elementem jest pewna liczba, a drugim pewien zbiór). Elementy zbioru nie muszą mieć tej samej natury. Podkreślmy jeszcze, że poprawnie utworzony zbiór ( jest to pewien obiekt matematyczny)- a więc jeden element (zbiór)- złożony z elementów, ale sam w sobie jest jednym zbiorem. Zbiory, gdy mają takie same elementy, to są równe, a więc jest to jeden i ten sam zbiór. |
Dla dowolnych <math>a,b</math>, mamy: <math>\left\{ a,b\right\}=\left\{ b ,a\right\}</math>. Teraz wprowadzimy obiekt, który ma własność przeciwną, obiekt złożony z dwóch składowych, rozróżniający każdą ze składowych z osobna, zwany parą uporządkowaną. | Dla dowolnych <math>a,b</math>, mamy: <math>\left\{ a,b\right\}=\left\{ b ,a\right\}</math>. Teraz wprowadzimy obiekt, który ma własność przeciwną, obiekt złożony z dwóch składowych, rozróżniający każdą ze składowych z osobna, zwany parą uporządkowaną. | ||
| Linia 119: | Linia 80: | ||
<math>\left(a _{1},a _{2} \right) =\left( b _{1},b_{2}\right), \hbox{ wtedy i tylko wtedy, gdy } a _{1}=b _{1}\hbox{ i } a _{2}=b _{2}</math>. | <math>\left(a _{1},a _{2} \right) =\left( b _{1},b_{2}\right), \hbox{ wtedy i tylko wtedy, gdy } a _{1}=b _{1}\hbox{ i } a _{2}=b _{2}</math>. | ||
| − | Powyższa własność mówi, że jeśli jedna para różni się od drugiej, choć na pierwszej, czy choć na drugiej współrzędnej, to te pary uporządkowane są różne. | + | Powyższa własność mówi, że jeśli jedna para różni się od drugiej, choć na pierwszej, czy choć na drugiej współrzędnej, to te pary uporządkowane są różne. |
| − | |||
| − | Ogólniej, <math>\left( a,b\right) \neq \left( b,a\right)</math>, jeśli tylko <math>a \neq b</math> | + | Np.: <math>\left( 1,2\right) \neq \left( 1,3\right)</math>, <math>\left( 1,2\right) \neq \left( 2,2\right)</math>, <math>\left( 1,2\right) \neq \left( 2,1\right)</math>. Ogólniej, <math>\left( a,b\right) \neq \left( b,a\right)</math>, jeśli tylko <math>a \neq b</math> (dla <math>a=b</math>, oczywiście <math>\left( a,a\right)= \left( a,a\right)</math> ). Tłumaczy to nazwę para '''uporządkowana'''. |
Zastanówmy się na koniec tego rozdziału, czy istnieje nieskończony ciąg zbiorów <math>\left( X _{n} \right)</math>, taki że: | Zastanówmy się na koniec tego rozdziału, czy istnieje nieskończony ciąg zbiorów <math>\left( X _{n} \right)</math>, taki że: | ||
Aktualna wersja na dzień 01:32, 6 mar 2018
Teoria zbiorów, zwana również teorią mnogości, została stworzona około połowy XIX wieku, przez niemieckiego matematyka Georga Cantora. Teoria mnogości to gałąź matematyki zajmująca się zbiorami - kolekcją obiektów.
Według Cantora każda kolekcja obiektów jest zbiorem. Wtedy te obiekty nazywamy elementami zbioru; i jeśli obiekt jest elementem zbioru , to zapisujemy to jako . Czytamy to również jako: element należy do zbioru . W przeciwnym przypadku, jeśli obiekt nie jest elementem zbioru , to zapisujemy to jako , i czytamy: nie należy do zbioru , albo nie jest elementem zbioru . Zbiory na ogół oznaczamy dużymi literami, np. . Skończone zbiory można definiować po przez wypisanie ich elementów (w nawiasach klamrowych na oznaczenie zbioru). Np. zbiór posiada trzy elementy: i . Zgodnie z powyższym możemy to zapisać , i przeczytać należy do zbioru , albo jest elementem zbioru . Podobnie możemy zapisać . Ale już np. - nie jest elementem zbioru . Inny przykład- "Kraków" "zbiór wszystkich miast Polski", bo Kraków jest miastem Polski. Aby zdefiniować zbiór, należy określić sposób rozpoznawania czy dany obiekt jest jest jego elementem, czy nie. Musimy wiedzieć z jakich elementów jest on złożony, a inne obiekty nie są jego elementami.
Dwa zbiory są sobie równe (takie same), jeśli posiadają dokładnie te same elementy. Jedynymi elementami zbioru są liczby naturalne i , tą samą własność ma zbiór , a więc , ale również , bo ostatni zbiór też ma dokładnie elementy i , oraz "zbiór liczb naturalnych ściśle pomiędzy a ". W definicji zbioru nie ma znaczenia kolejność, w jakiej wymienione są jego elementy, ani to czy element się powtarza w zbiorze.
Zbiory można definiować na wiele sposobów. Najprostszym sposobem jest wypisanie jego elementów. Strategia ta zawodzi jednak w odniesieniu do zbiorów nieskończonych - nie jesteśmy w stanie wypisać wszystkich liczb naturalnych. Zbiór liczb naturalnych zapisujemy nieformalnie jako: Podobnie, zbiór liczb naturalnych parzystych zapisujemy jako: Przed wielokropkiem należy wypisać co najmniej tyle początkowych elementów, tak aby nie wprowadzać nieporozumień, żeby nikt nie zrozumiał (i to poprawnie) inaczej ten zbiór niż chcemy.
Innym sposobem definiowania zbiorów jest rozważanie zbioru wszystkich elementów spełniających daną własność. Na przykład zbiór liczb parzystych może być zdefiniowany jako: Np. , bo jest liczbą parzystą. Bardziej ogólnie, definicje te wyglądają tak: . W skład powyższego zbioru wchodzą dokładnie te elementy, które spełniają warunek pojawiający się w definicji tegoż zbioru. Kolejny przykład:
,
, bo Kraków jest miastem Polski. , bo Berlin nie leży w Polsce.
Inkluzja, równość zbiorów:
Pomiędzy zbiorem liczb parzystych a zbiorem wszystkich liczb naturalnych występuje oczywista zależność. Każda liczba parzysta jest liczbą naturalną, co, ujęte w języku zbiorów, oznacza, że każdy element zbioru liczb parzystych jest elementem zbioru liczb naturalnych. Zbiór liczb parzystych jest podzbiorem zbioru liczb naturalnych. Ogólniej, dla dwóch zbiorów , , jeśli każdy element zbioru jest elementem zbioru , to nazywamy to zawieraniem zbiorów, i czytamy: zbiór zawiera się w zbiorze , co zapisujemy . Mówimy wtedy też, że zbiór jest podzbiorem zbioru ( jest nadzbiorem ). Zawieranie zbiorów nazywane jest też inkluzją.Np.: , ale też oraz "zbiór wszystkich psów" "zbiór wszystkich zwierząt".
Dla dowolnego zbioru , mamy: (bo każdy element zbioru , jest elementem ). Wspomnieliśmy wcześniej, że dwa zbiory są sobie równe, wtedy i tylko wtedy, kiedy posiadają dokładnie takie same elementy. Nawiązuje do tego poniższe twierdzenie:
Często, zależy nam na określeniu znaczącym, że jeden zbiór jest podzbiorem drugiego, i że zbiory te nie są sobie równe. Używamy wtedy symbolu , w poniższy sposób:
ĆWICZENIE:
Dla poniższych par zbiorów, określ, czy są sobie równe, oraz czy jeden z nich jest podzbiorem drugiego:
Rozwiązanie:
Zarówno , jak i , dzielą liczbę , a więc . Również dzieli , czyli jest elementem zbioru prawego, a nie jest elementem zbioru lewego, a więc te zbiory są różne, i .
Liczba jest liczbą naturalną, a więc elementem zbioru lewego, a nie dzieli , a więc nie jest elementem zbioru prawego, a więc te zbiory są różne. Pozostaje sprawdzić, czy prawy zbiór jest podzbiorem zbioru liczb naturalnych. Mamy, że dzieli . Zatem jest elementem zbioru prawego, a nie jest liczbą naturalną. Czyli lewy zbiór nie zawiera się w prawym, i również prawy zbiór nie zawiera się w lewym.
OPERACJE NA ZBIORACH:
Sumą dwóch zbiorów , to zbiór oznaczany jako , złożony dokładnie ze wszystkich elementów zbioru , oraz ze wszystkich elementów zbioru .
Np. .
Iloczynem (częścią wspólną, przekrojem ), dwóch zbiorów , to zbiór oznaczany jako , złożony dokładnie z tych elementów zbioru , które jednocześnie są elementami zbioru .
Np. , - zbiór nieposiadający elementów, zwany dalej zbiorem pustym.
Różnicą dwóch zbiorów , to zbiór oznaczany jako , złożony dokładnie z tych elementów zbioru , które nie są elementami zbioru .
Np. , .
Fakt. Jeśli mamy, że , to wtedy:
.
.
.
Np.: , .
Dla dowolnego zbioru , zachodzi: , oraz . - jest to zbiór złożony ze wszystkich elementów zbioru , oraz ze wszystkich elementów zbioru , czyli ze wszystkich elementów zbioru , co potwierdza równość . Natomiast - jest to zbiór złożony dokładnie z tych elementów zbioru , które są elementami zbioru , czyli ze wszystkich elementów zbioru , co potwierdza równość .
Zbiory złożone ze zbiorów i inne podstawowe sprawy:
Elementami zbiorów mogą być inne zbiory, np.: . Ten zbiór posiada elementów, np. . Oczywiście, to zbiór jednoelementowy złożony z , dalej to zbiór jednoelementowy złożony z elementu - poprzedniego zbioru, i to zbiór jednoelementowy złożony z poprzedniego elementu, mamy . Podobnie, , oraz . Takie zbiory (złożone ze zbiorów) nazywamy czasem rodzinami zbiorów. Zgodnie ze założeniami Cantora -każda kolekcja obiektów jest zbiorem. Możemy zatem mówić, np. o zbiorze złożonym ze funkcji, a także o dowolnym zbiorze dwuelementowym (np. takim, którego pierwszym elementem jest pewna liczba, a drugim pewien zbiór). Elementy zbioru nie muszą mieć tej samej natury. Podkreślmy jeszcze, że poprawnie utworzony zbiór ( jest to pewien obiekt matematyczny)- a więc jeden element (zbiór)- złożony z elementów, ale sam w sobie jest jednym zbiorem. Zbiory, gdy mają takie same elementy, to są równe, a więc jest to jeden i ten sam zbiór.
Dla dowolnych , mamy: . Teraz wprowadzimy obiekt, który ma własność przeciwną, obiekt złożony z dwóch składowych, rozróżniający każdą ze składowych z osobna, zwany parą uporządkowaną.
Para uporządkowana , to kolekcja dwóch elementów (zwanych współrzędnymi), rozróżniająca każdą ze współrzędnych z osobna, tzn. o własności:
.
Powyższa własność mówi, że jeśli jedna para różni się od drugiej, choć na pierwszej, czy choć na drugiej współrzędnej, to te pary uporządkowane są różne.
Np.: , , . Ogólniej, , jeśli tylko (dla , oczywiście ). Tłumaczy to nazwę para uporządkowana.
Zastanówmy się na koniec tego rozdziału, czy istnieje nieskończony ciąg zbiorów , taki że:
Postaram się uzasadnić , że takich ciągów nie może być w teorii mnogości. Zauważmy, że zgodnie z intuicją, zbiór jest poprawnie określony, gdy wiadomo z jakich elementów jest złożony. Rozważmy, przez chwilę, taki ciąg zbiorów. jest poprawnie utworzonym zbiorem, więc jest złożonym z pewnych elementów, jednym jego elementem jest zbiór . Co to za zbiór? Jednym jego elementem jest zbiór . Co to za zbiór ? Jednym jego elementem jest zbiór - itd. Nie możemy robić tego procesu w nieskończoność, bo nie zamkniemy określenia elementów, tych że zbiorów. Zatem takich ciągów (nieskończonych) nie ma.